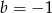Zadanie nr 4414640
Dane są funkcje liniowe 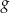 i
i 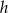 określone wzorami:
określone wzorami: 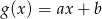 i
i 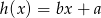 . Wiadomo, że funkcja
. Wiadomo, że funkcja  jest rosnąca, a
jest rosnąca, a  malejąca.
malejąca.
- Wyznacz pierwszą współrzędna punktu przecięcia wykresów tych funkcji.
- Oblicz liczby
 i
i  wiedząc, że wykresy funkcji
wiedząc, że wykresy funkcji 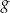 i
i 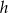 są prostymi prostopadłymi, a punkt ich przecięcia leży na osi
są prostymi prostopadłymi, a punkt ich przecięcia leży na osi 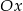 .
.
Rozwiązanie
Z podanych informacji wiemy, że 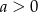 i
i 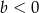 .
.
- Liczymy (porównujemy
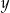 -ki)
-ki) 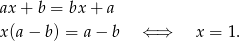
Powyżej skorzystaliśmy z faktu, że
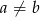 , który wynika z nierówności
, który wynika z nierówności 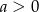 i
i 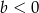 .
.
Odpowiedź: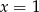
- Wiemy teraz dodatkowo, że
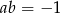 oraz, że punkt wspólny wykresów leży na osi
oraz, że punkt wspólny wykresów leży na osi 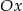 . Z poprzedniego podpunktu wiemy, pierwsza współrzędna tego punktu jest równa 1, czyli musi on mieć współrzędne
. Z poprzedniego podpunktu wiemy, pierwsza współrzędna tego punktu jest równa 1, czyli musi on mieć współrzędne 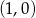 . Podstawiamy te liczby do wzoru pierwszej funkcji.
. Podstawiamy te liczby do wzoru pierwszej funkcji. 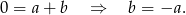
Z równości
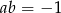 mamy więc
mamy więc 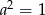 , czyli
, czyli 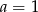 i
i 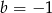 (obrazek).
(obrazek). 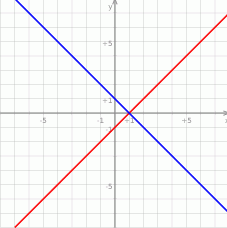
Odpowiedź: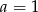 ,
,