/Szkoła średnia/Funkcje - wykresy/Liniowy

Zadanie nr 5413941

Dodaj do ulubionych
Dodaj do rozwiązanych

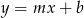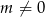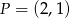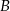Wykres funkcji liniowej y = mx + b dla m ⁄= 0 przechodzi przez punkt P = (2,1) i przecina oś x w punkcie B . Wyraź odległość punktu 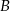B od początku układu współrzędnych jako funkcje parametru 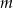m . Wyznacz miejsce zerowe tej funkcji i naszkicuj jej wykres.

Rozwiązanie

Zacznijmy od szkicowego rysunku.

PIC

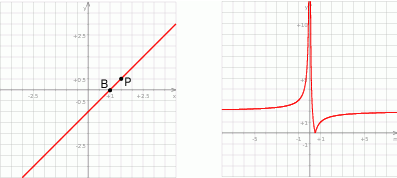
Ponieważ punkt 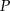P należy do danej prostej to

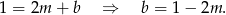
1 = 2m + b ⇒ b = 1 − 2m .

Wyliczmy punkt przecięcia się tej prostej z osią x .

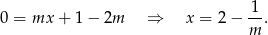
1 0 = mx + 1 − 2m ⇒ x = 2 − --. m

Szukana funkcja to zatem 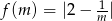-1 f (m) = |2 − m | . Jej miejsce zerowe to 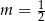1 m = 2 . Pozostało naszkicować jej wykres. Jest to hiperbola 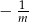− m1 przesunięta o dwie jednostki w górę i jej część znajdująca się pod osią x jest odbita względem tej osi.  
Odpowiedź: 1 m = 2

Wersja PDF