Zadanie nr 6261702

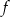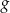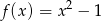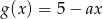Wyznacz wszystkie wartości parametru , dla których wykresy funkcji i , określonych wzorami f(x) = x2 − 1 oraz g (x) = 5 − ax , przecinają w dwóch punktach znajdujących się powyżej osi 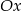układu współrzędnych.

Rozwiązanie

Sposób I

Próbujemy wyznaczyć punkt wspólny wykresów danych funkcji.

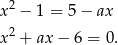
x2 − 1 = 5 − ax x2 + ax − 6 = 0.

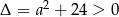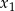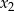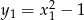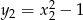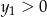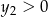Zauważmy, że równanie to ma zawsze dwa rozwiązania, bo Δ = a2 + 24 > 0 . Jeżeli oznaczmy te rozwiązania przez x 1 i x 2 , to odpowiadają im y = x2 − 1 1 1 oraz 2 y2 = x2 − 1 . Nasze zadanie polega na ustaleniu kiedy y1 > 0 i y2 > 0 . Będziemy chcieli te warunki zapisać przy pomocy wzorów Viète’a

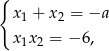
{ x1 + x2 = −a x x = − 6, 1 2

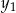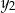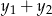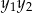więc dodatniość i zamieniamy na równoważny warunek dodatniości y1 + y2 i y 1y 2 . Musimy więc rozwiązać układ nierówności

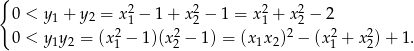
{ 0 < y1 + y2 = x21 − 1 + x22 − 1 = x21 + x22− 2 0 < y y = (x2 − 1)(x 2− 1) = (x x )2 − (x2+ x2)+ 1. 1 2 1 2 1 2 1 2

W powyższym układzie dwukrotnie występuje

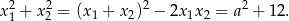
x2 + x2 = (x + x )2 − 2x x = a2 + 12. 1 2 1 2 1 2

Podstawiamy to wyrażenie do układu.

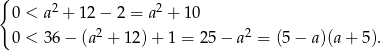
{ 0 < a2 + 12− 2 = a2 + 10 0 < 36 − (a2 + 12) + 1 = 25 − a2 = (5− a )(a+ 5 ).

Mamy stąd 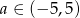a ∈ (− 5,5) .

Sposób II

Spróbujmy naszkicować opisaną sytuację.

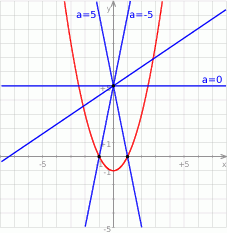
Wszystkie proste postaci 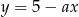y = 5− ax przechodzą przez punkt 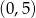(0,5) . Jeżeli 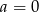a = 0 , to mamy poziomą prostą, która przecina parabolę na poziomie 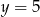y = 5 , więc wyraźnie powyżej osi 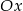. Jeżeli natomiast będzie rosnąć lub maleć, to prosta 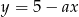zacznie się obracać (w jedną lub drugą stronę) i punkty wspólne z parabolą będą tak długo powyżej osi 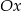jak długo prosta nie znajdzie się w jednym z dwóch skrajnych położeń, gdy przecina parabolę na osi 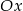, czyli w punktach 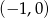(−1 ,0) lub (1,0) . 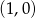Jak łatwo sprawdzić te skrajne położenia odpowiadają odpowiednio wartościom 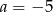a = −5 i a = 5 . 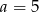W takim razie punkty wspólne danej paraboli i prostej są powyżej osi 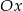dla a ∈ (− 5,5) .
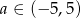Odpowiedź: