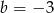/Szkoła średnia/Funkcje - wykresy/Liniowy

Zadanie nr 6738955

Dodaj do ulubionych
Dodaj do rozwiązanych

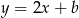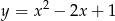Wyznacz wzór funkcji y = 2x+ b , której wykres ma dokładnie jeden punkt wspólny z wykresem y = x2 − 2x + 1 .

Rozwiązanie

Sposób I

Musimy sprawdzić kiedy (dla jakiego 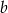b ) równanie

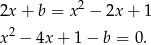
2 2x+ b = x − 2x + 1 x2 − 4x+ 1− b = 0.

ma dokładnie jedno rozwiązanie. Tak będzie gdy 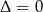Δ = 0 .

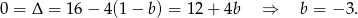
0 = Δ = 16− 4(1− b) = 12 + 4b ⇒ b = − 3.

Sposób II

Prosta 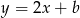y = 2x + b ma z parabolą jeden punkt wspólny wtedy, gdy jest do niej styczna. Patrzymy zatem, w którym punkcie styczna do 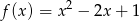f(x ) = x2 − 2x + 1 ma współczynnik kierunkowy 2 (tak jak nasza prosta).

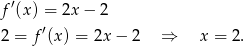
f ′(x) = 2x− 2 2 = f′(x) = 2x − 2 ⇒ x = 2.

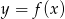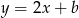Zatem chcemy, by wartości y = f (x) oraz y = 2x + b były takie same w x = 2 .

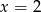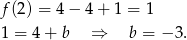
f (2) = 4− 4+ 1 = 1 1 = 4+ b ⇒ b = − 3.

Na koniec rysunek całej sytuacji.

PIC

 
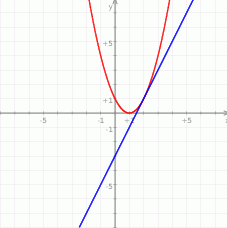
Odpowiedź: b = − 3

Wersja PDF