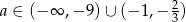/Szkoła średnia/Funkcje - wykresy/Liniowy

Zadanie nr 8390632

Dodaj do ulubionych
Dodaj do rozwiązanych

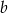Dla jakich wartości parametru a istnieje b takie, że prosta 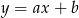y = ax + b przechodzi przez punkt 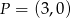P = (3,0) i przecina parabolę 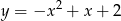y = −x 2 + x+ 2 w dwóch punktach o dodatnich odciętych?

Rozwiązanie

To że prosta ma przechodzić przez punkt 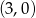(3,0) oznacza, że

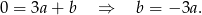
0 = 3a + b ⇒ b = − 3a.

Przecięcia tej prostej z podaną parabolą to rozwiązania równania

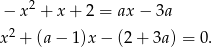
2 − x + x + 2 = ax− 3a x 2 + (a − 1)x − (2 + 3a ) = 0.

Na początku sprawdźmy kiedy to równanie ma dwa rozwiązania

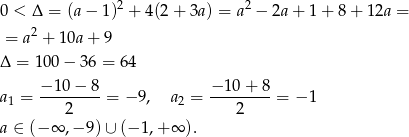
0 < Δ = (a − 1)2 + 4(2 + 3a) = a2 − 2a + 1 + 8 + 12a = 2 = a + 10a + 9 Δ = 100 − 36 = 6 4 a1 = −-10-−-8-= − 9, a2 = −-10+--8-= − 1 2 2 a ∈ (− ∞ ,− 9)∪ (− 1,+ ∞ ).

Pozostało sprawdzić, kiedy oba rozwiązania są dodatnie. Tak będzie jeżeli zarówno ich iloczyn jak i suma będą dodatnie. Na mocy wzorów Viète’a mamy

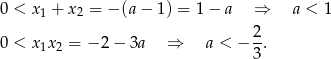
0 < x + x = − (a− 1) = 1 − a ⇒ a < 1 1 2 0 < x x = − 2 − 3a ⇒ a < − 2. 1 2 3

Łącząc wszystkie otrzymane nierówności mamy 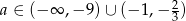a ∈ (− ∞ ,− 9) ∪ (− 1,− 23) .  
Odpowiedź: a ∈ (− ∞ ,− 9) ∪ (−1 ,− 2) 3

Wersja PDF