Zadanie nr 8670332
Funkcja 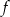 określona jest wzorem
określona jest wzorem 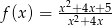 . Znajdź taki wektor
. Znajdź taki wektor ![→u = [p,0]](https://img.zadania.info/zad/8670332/HzadT2x.gif) , aby po przesunięciu wykresu funkcji
, aby po przesunięciu wykresu funkcji 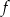 o wektor
o wektor 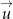 otrzymać wykres funkcji parzystej. Podaj wzór funkcji, której wykres otrzymamy po przesunięciu wykresu funkcji
otrzymać wykres funkcji parzystej. Podaj wzór funkcji, której wykres otrzymamy po przesunięciu wykresu funkcji 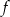 o znaleziony wektor.
o znaleziony wektor.
Rozwiązanie
Na początku zapiszmy podany wzór funkcji w trochę prostszej postaci
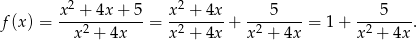
Jeżeli przsuniemy tę funkcję o wektor ![→ u = [p ,0]](https://img.zadania.info/zad/8670332/HzadR1x.gif) , to otrzymamy funkcję
, to otrzymamy funkcję
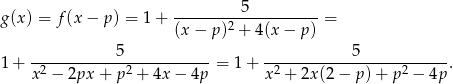
Pozostało sprawdzić, kiedy (dla jakiego 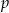 ) ta funkcja jest parzysta.
) ta funkcja jest parzysta.
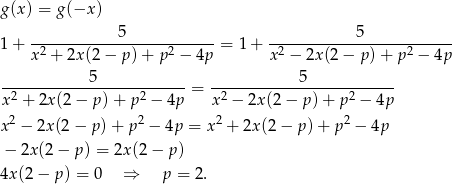
Żeby było jasne, ostatnia równość 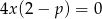 musi być spełniona dla wszystkich
musi być spełniona dla wszystkich  z dziedziny funkcji (jest to tak naprawdę równość dwóch funkcji, a nie liczb), dlatego z równości tej wynika, że
z dziedziny funkcji (jest to tak naprawdę równość dwóch funkcji, a nie liczb), dlatego z równości tej wynika, że 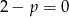 , a nie np.
, a nie np. 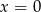 .
.
Mamy wtedy
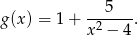
Na koniec, dla ciekawskich, wykresy obu funkcji.
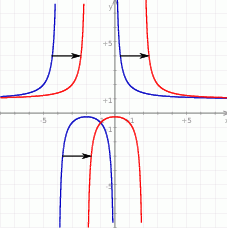
Odpowiedź: 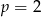 , wzór funkcji:
, wzór funkcji: 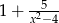 .
.

