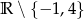Zadanie nr 4272119
Wykres funkcji 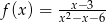 przesunięto o wektor
przesunięto o wektor ![→ u = [− 2;1]](https://img.zadania.info/zad/4272119/HzadT1x.gif) , a następnie przesunięty wykres odbito symetrycznie względem początku układu współrzędnych. Otrzymano wykres pewnej funkcji
, a następnie przesunięty wykres odbito symetrycznie względem początku układu współrzędnych. Otrzymano wykres pewnej funkcji 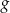 . Znajdź wzór funkcji
. Znajdź wzór funkcji 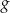 i wyznacz jej dziedzinę.
i wyznacz jej dziedzinę.
Rozwiązanie
Korzystamy ze wzoru na przesunięcie funkcji 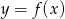 o wektor
o wektor ![→ v = [a,b]](https://img.zadania.info/zad/4272119/HzadR1x.gif) :
:
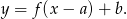
Sposób I
W naszej sytuacji, po przesunięciu, otrzymamy funkcję
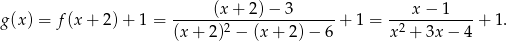
Odbicie wykresu względem początku układu, to to samo co wykonanie dwóch odbić: najpierw względem osi 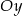 , potem względem
, potem względem 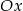 . Przekształceniu temu odpowiada zmiana wzoru:
. Przekształceniu temu odpowiada zmiana wzoru:
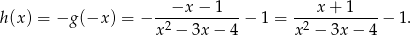
Aby wyznaczyć dziedzinę tej funkcji, musimy sprawdzić, dla jakich  -ów mianownik się zeruje.
-ów mianownik się zeruje.
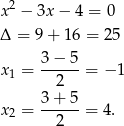
Zatem dziedzina to zbiór 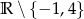 .
.
Sposób II
Znajdźmy pierwiastki mianownika danego wzoru funkcji.
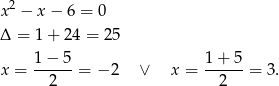
Zatem
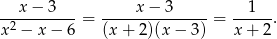
Musimy być jednak ostrożni i pamiętać, że dziedziną powyższej funkcji jest 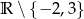 .
.
Po przesunięciu o wektor ![[− 2;1]](https://img.zadania.info/zad/4272119/HzadR13x.gif) otrzymamy funkcję
otrzymamy funkcję
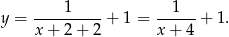
Ponieważ przesunęliśmy wykres w lewo o dwie jednostki, dziedziną tej funkcji będzie zbiór 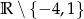 .
.
Podobnie jak poprzednio zauważamy, że odbiciu względem początku układu współrzędnych odpowiada zmiana wzoru funkcji postaci 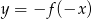 , czyli otrzymamy funkcję
, czyli otrzymamy funkcję
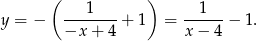
Dziedziną będzie zbiór 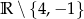 .
.
Na zakończenie, dla ciekawskich, wszystkie trzy wykresy.
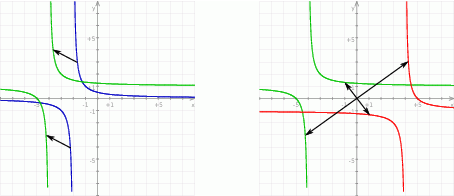
Odpowiedź: 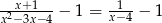 , Dziedzina:
, Dziedzina: