/Szkoła średnia/Funkcje - wykresy/Wykładniczy

Zadanie nr 3831771

Dodaj do ulubionych
Dodaj do rozwiązanych

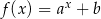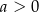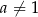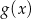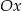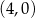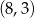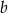Wykres funkcji wykładniczej x f(x ) = a + b (gdzie a > 0 i a ⁄= 1 ) przesunięto o 4 jednostki w prawo i 2 jednostki w dół. W rezultacie otrzymano wykres funkcji g(x) , który przecina oś Ox w punkcie (4,0) oraz przechodzi przez punkt (8,3) . Wyznacz a i b oraz rozwiąż nierówność f (x) ≤ 5 .

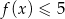Rozwiązanie

Przesuwając wykres 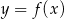y = f(x) o 4 jednostki w prawo otrzymujemy wykres funkcji 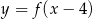y = f(x − 4 ) . Następnie przesuwamy ten wykres o dwie jednostki w dół i otrzymujemy wykres 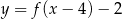y = f(x − 4) − 2 . Zatem

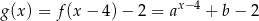
g(x ) = f(x − 4) − 2 = ax− 4 + b− 2

oraz

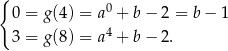
{ 0 = g(4) = a0 + b − 2 = b− 1 4 3 = g(8) = a + b − 2.

Z pierwszego równania 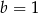b = 1 , a z drugiego

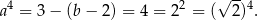
√ -- a4 = 3 − (b − 2) = 4 = 22 = ( 2)4.

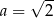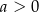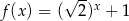Zatem √ -- a = 2 (bo z założenia a > 0 ) i √ -- f(x) = ( 2)x + 1 . Szkicujemy teraz wykres tej funkcji wykładniczej oraz prostą y = 5 .

PIC

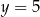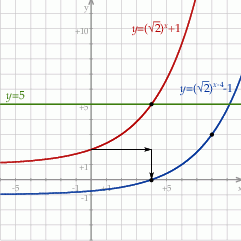
Zauważmy, że

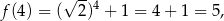
√ -- f(4) = ( 2)4 + 1 = 4 + 1 = 5,

więc wykres 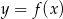y = f (x) przecina prostą 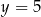y = 5 w punkcie 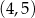(4,5) . W takim razie rozwiązaniem nierówności 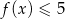f (x) ≤ 5 jest przedział

(− ∞ ,4⟩.

 
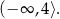
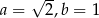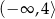Odpowiedź: √ -- a = 2,b = 1 , (− ∞ ,4⟩ .

Wersja PDF