Zadanie nr 4713954
Wykres funkcji 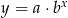 powstaje z wykresu funkcji
powstaje z wykresu funkcji 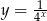 przez jednokładność o środku w punkcie
przez jednokładność o środku w punkcie 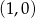 i skali
i skali 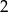 . Wyznacz liczby
. Wyznacz liczby  i
i 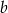 .
.
Rozwiązanie
Możemy zacząć od naszkicowania opisanej sytuacji.
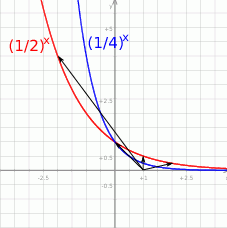
Ponieważ do wyznaczenia mamy dwa parametry, potrzebujemy dwóch punktów na wykresie funkcji 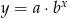 . Nie jest trudno je znaleźć: jeżeli weźmiemy jakikolwiek punkt
. Nie jest trudno je znaleźć: jeżeli weźmiemy jakikolwiek punkt 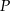 na wykresie funkcji
na wykresie funkcji 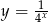 , to jest on środkiem odcinka o końcach
, to jest on środkiem odcinka o końcach 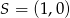 i
i 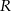 , gdzie
, gdzie 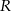 jest odpowiadającym punktem wykresu funkcji
jest odpowiadającym punktem wykresu funkcji 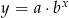 . Wystarczy zatem wybrać dwa proste punkty
. Wystarczy zatem wybrać dwa proste punkty 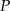 i wyliczyć odpowiadające punkty
i wyliczyć odpowiadające punkty 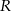 .
.
Jeżeli weźmiemy 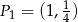 to ma to być środek odcinka o końcach
to ma to być środek odcinka o końcach 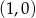 i
i 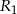 , więc
, więc
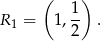
Jeżeli weźmiemy 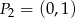 to ma to być środek odcinka o końcach
to ma to być środek odcinka o końcach 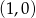 i
i 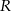 , więc
, więc
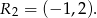
Podstawiając współrzędne punktów 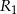 i
i 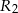 do wzoru
do wzoru 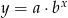 otrzymujemy układ równań
otrzymujemy układ równań
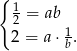
Mnożąc równania stronami mamy 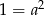 . Z rysunku jest jasne, że
. Z rysunku jest jasne, że  musi być dodatnie (wykres ma być powyżej osi
musi być dodatnie (wykres ma być powyżej osi 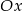 ), więc
), więc 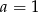 . Stąd
. Stąd 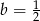 .
.
Odpowiedź: