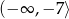Zadanie nr 7485369
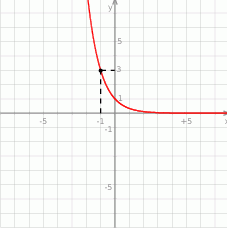
Na rysunku przedstawiono wykres pewnej funkcji wykładniczej 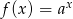 dla
dla 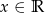 .
.
Wykres ten przekształcono w symetrii środkowej względem punktu 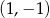 , a następnie w symetrii osiowej względem prostej
, a następnie w symetrii osiowej względem prostej 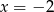 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 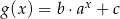 .
.
- Wyznacz liczby
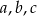 i naszkicuj wykres funkcji
i naszkicuj wykres funkcji 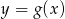 .
. - Odczytaj z wykresu rozwiązanie nierówności
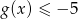 .
.
Rozwiązanie
Rozpocznijmy od wyznaczenia  . Z wykresu widzimy, że
. Z wykresu widzimy, że 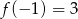 , czyli
, czyli
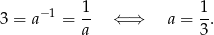
- Szukamy funkcji postaci
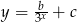 , więc wystarczy znaleźć dwa punkty na jej wykresie, aby wyznaczyć
, więc wystarczy znaleźć dwa punkty na jej wykresie, aby wyznaczyć 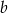 i
i  (mamy dwie niewiadome, więc potrzebujemy dwóch równań). Można wybrać różne punkty – my zobaczymy na co przejdą punkty
(mamy dwie niewiadome, więc potrzebujemy dwóch równań). Można wybrać różne punkty – my zobaczymy na co przejdą punkty 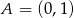 i
i 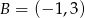 .
. 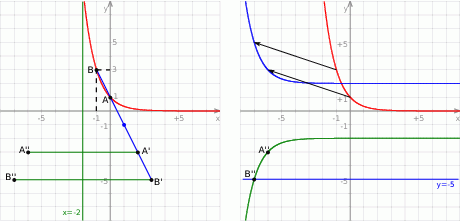
Najpierw symetria środkowa względem punktu
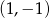 . Szukamy punktów
. Szukamy punktów 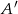 i
i 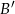 takich, żeby punkt
takich, żeby punkt 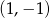 był środkiem odcinków
był środkiem odcinków 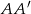 i
i 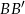 .
. 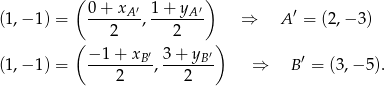
Teraz znajdujemy obrazy
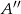 i
i 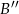 punktów
punktów 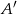 i
i 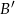 w symetrii względem prostej
w symetrii względem prostej 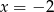 . Punkty te będą miały takie same drugie współrzędne jak punkty
. Punkty te będą miały takie same drugie współrzędne jak punkty 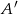 i
i 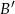 , a ich pierwsze współrzędne muszą być takie, żeby środki odcinków
, a ich pierwsze współrzędne muszą być takie, żeby środki odcinków 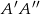 i
i 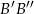 leżały na prostej
leżały na prostej 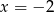 . Mamy więc
. Mamy więc 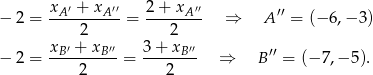
Teraz łatwo wyznaczyć liczby
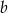 i
i  – podstawiamy współrzędne punktów
– podstawiamy współrzędne punktów 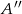 i
i 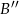 do wzoru funkcji
do wzoru funkcji 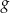 .
. 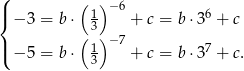
Porównując
 z obu równań mamy
z obu równań mamy 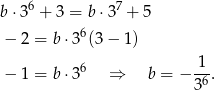
Zatem
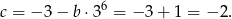
Odpowiedź: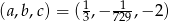
- Ponieważ
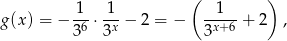
wykres funkcji
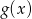 powstaje z wykresu funkcji
powstaje z wykresu funkcji 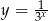 przez przesunięcie o wektor
przez przesunięcie o wektor ![[− 6,2]](https://img.zadania.info/zad/7485369/HzadR40x.gif) , a następnie odbicie względem osi
, a następnie odbicie względem osi 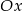 . Bez trudu szkicujemy wykres.
. Bez trudu szkicujemy wykres. Z wykresu widać, że rozwiązaniem nierówności
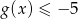 jest przedział
jest przedział 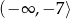 .
.
Odpowiedź: