Zadanie nr 8666204
Wykres funkcji 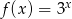 przesunięto najpierw o wektor
przesunięto najpierw o wektor ![→ v1 = [1,− 3]](https://img.zadania.info/zad/8666204/HzadT1x.gif) , potem o wektor
, potem o wektor ![→ v 2 = [− 2,1]](https://img.zadania.info/zad/8666204/HzadT2x.gif) , a na koniec o wektor
, a na koniec o wektor 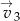 . W wyniku tej operacji otrzymano przedstawiony na poniższym rysunku wykres funkcji
. W wyniku tej operacji otrzymano przedstawiony na poniższym rysunku wykres funkcji 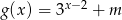 .
.
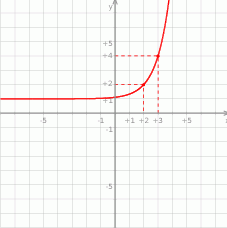
- Podaj wartość
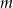 .
. - Wyznacz współrzędne wektora
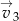 .
.
Rozwiązanie
- Współczynnik
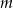 możemy wyznaczyć podstawiając do podanego wzoru jeden z punktów zaznaczonych na wykresie, np.
możemy wyznaczyć podstawiając do podanego wzoru jeden z punktów zaznaczonych na wykresie, np. 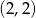 .
. 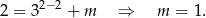
Mogliśmy też od razu zgadnąć, że wykres funkcji
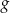 jest przesunięty względem wykresu
jest przesunięty względem wykresu 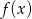 o jedną jednostkę do góry (bo przykleja się do prostej
o jedną jednostkę do góry (bo przykleja się do prostej 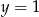 zamiast do
zamiast do 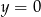 ).
).
Odpowiedź: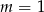
- Oznaczmy
![→ v 3 = [p,q]](https://img.zadania.info/zad/8666204/HzadR8x.gif) . Z poprzedniego podpunktu wiemy, że
. Z poprzedniego podpunktu wiemy, że 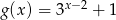 , więc wykres tej funkcji powstaje z wykresu funkcji
, więc wykres tej funkcji powstaje z wykresu funkcji 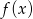 przez przesunięcie o wektor
przez przesunięcie o wektor ![[2,1]](https://img.zadania.info/zad/8666204/HzadR11x.gif) . Z drugiej strony wiemy, że wykresy te są przesunięte względem siebie o
. Z drugiej strony wiemy, że wykresy te są przesunięte względem siebie o ![→ → → v 1 + v2 + v 3 = [1,− 3]+ [− 2,1] + [p,q] = [p− 1,q− 2].](https://img.zadania.info/zad/8666204/HzadR12x.gif)
Daje to nam równanie
![[2,1] = [p− 1,q− 2],](https://img.zadania.info/zad/8666204/HzadR13x.gif)
skąd
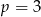 i
i 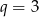 .
.
Odpowiedź:![→v = [3 ,3] 3](https://img.zadania.info/zad/8666204/HzadR16x.gif)

