Zadanie nr 5083137
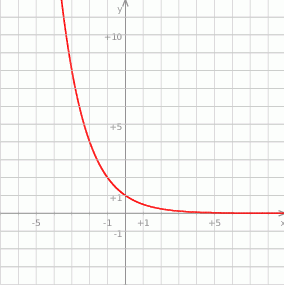
Na rysunku przedstawiono wykres pewnej funkcji wykładniczej 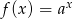 dla
dla 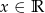
- Narysuj wykres funkcji
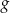 , który jest obrazem wykresu funkcji
, który jest obrazem wykresu funkcji 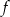 w przesunięciu o wektor
w przesunięciu o wektor ![→ u = [2,− 1]](https://img.zadania.info/zad/5083137/HzadT5x.gif) .
. - Wyznacz
 i zapisz wzór funkcji
i zapisz wzór funkcji 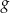 otrzymanej w wyniku tego przesunięcia.
otrzymanej w wyniku tego przesunięcia. - Odczytaj z wykresu zbiór wszystkich argumentów, dla których
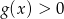 .
.
Rozwiązanie
- Wykres funkcji
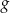 powstaje z
powstaje z 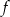 przez przesunięcie o dwie jednostki w prawo i jedną w dół – niebieski wykres na rysunku.
przez przesunięcie o dwie jednostki w prawo i jedną w dół – niebieski wykres na rysunku. 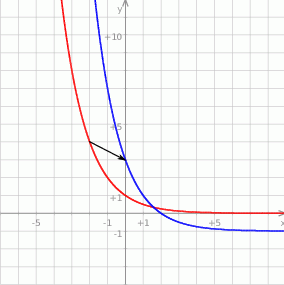
- Na wykresie w treści zadania widać, że
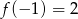 , tzn.
, tzn. 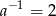 . Stąd
. Stąd 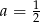 . Aby napisać wzór funkcji
. Aby napisać wzór funkcji 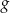 korzystamy ze wzoru na przesunięcie funkcji
korzystamy ze wzoru na przesunięcie funkcji 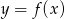 o wektor
o wektor ![→v = [a,b]](https://img.zadania.info/zad/5083137/HzadR8x.gif) :
: 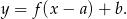
W naszej sytuacji
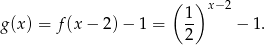
Odpowiedź: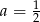 ,
, 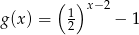
- Odczytujemy z wykresu:
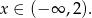
Odpowiedź: