/Konkursy

Zadanie nr 1068521

Dodaj do ulubionych
Dodaj do rozwiązanych

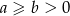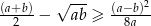Udowodnij, że jeżeli a ≥ b > 0 to (a+b-) √ --- (a−b-)2- 2 − ab ≥ 8a .

Rozwiązanie

Zauważmy, że lewa strona nierówności jest pełnym kwadratem, dokładniej

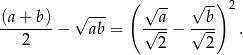
( √ -- √ -) 2 (a-+-b) √ --- --a- ---b 2 − ab = √ 2-− √ 2- .

Daną nierówność możemy więc przekształcić następująco (korzystamy z założenia 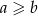a ≥ b ):

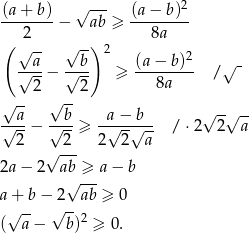
√ --- 2 (a-+-b) − ab ≥ (a−--b)- 2 8a ( √ -- √ -) 2 2 √--a− √-b- ≥ (a-−-b)- /√ - 2 2 8a √ -- √ -- --a- --b- --a−--b- √ -√ -- √ 2-− √ 2-≥ 2 √ 2√a-- / ⋅2 2 a √ --- 2a − 2 ab ≥ a− b √ --- a + b− 2--ab ≥ 0 (√a--− √ b)2 ≥ 0.

Ostatnia nierówność jest oczywiście prawdziwa, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też jest prawdziwa.

Wersja PDF