/Konkursy

Zadanie nr 1080589

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że dla dowolnych dodatnich liczb 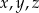x,y ,z spełniona jest nierówność

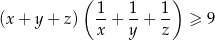
( 1 1 1 ) (x + y + z) -+ --+ -- ≥ 9 x y z

Rozwiązanie

Przekształcamy nierówność w sposób równoważny (wymnażamy nawiasy z lewej strony).

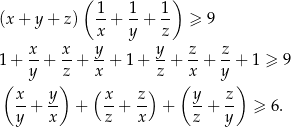
( ) (x + y + z) 1-+ 1-+ 1- ≥ 9 x y z x- x- y- y- z- -z 1+ y + z + x + 1 + z + x + y + 1 ≥ 9 ( ) ( ) ( ) x-+ y- + x-+ z- + y+ z- ≥ 6. y x z x z y

Sposób I

Korzystamy z prostej do uzasadnienia nierówności

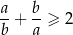
a-+ b-≥ 2 b a

prawdziwej dla dowolnych liczb dodatnich 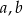a,b . Na mocy tej nierówności rzeczywiście

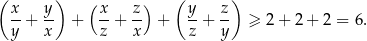
( ) ( ) ( ) x-+ y- + x-+ z- + y-+ z- ≥ 2+ 2 + 2 = 6. y x z x z y

Sposób II

Korzystamy z nierówności między średnimi: arytmetyczną i geometryczną dla 6 liczb

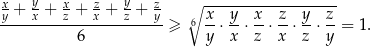
x y x z y z ∘ ------------------- y +-x-+-z-+-x-+--z +-y- 6 x- y- x- z- y- z- 6 ≥ y ⋅x ⋅ z ⋅ x ⋅z ⋅y = 1.

A to jest oczywiście nierówność, którą mieliśmy udowodnić.

Sposób III

Przekształcamy nierówność dalej.

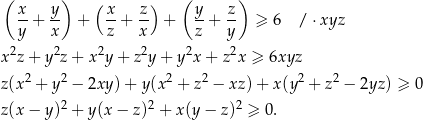
( ) ( ) x y (x z) y z --+ -- + --+ -- + -+ -- ≥ 6 / ⋅xyz y x z x z y x2z + y2z + x2y + z2y + y2x + z2x ≥ 6xyz 2 2 2 2 2 2 z(x + y − 2xy) + y(x + z − xz )+ x (y + z − 2yz ) ≥ 0 z(x − y)2 + y(x − z)2 + x(y − z)2 ≥ 0.

Ta nierówność jest oczywiście spełniona (bo 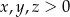x,y ,z > 0 ), a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musiała być spełniona.

Sposób IV

Korzystamy z nierówności Jensena

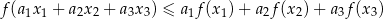
f(a1x1 + a2x2 + a3x3) ≤ a1f (x1)+ a2f(x2) + a3f(x3)

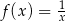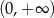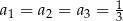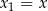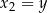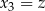dla funkcji wypukłej 1 f(x ) = x na przedziale (0,+ ∞ ) , współczynników a1 = a 2 = a3 = 13 oraz x1 = x , x2 = y , x3 = z . Mamy zatem

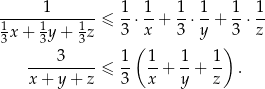
------1-------≤ 1-⋅ 1-+ 1-⋅ 1-+ 1-⋅ 1 13x + 13y + 13z 3 x 3 y 3 z ( ) ----3-----≤ 1- 1-+ 1-+ 1- . x+ y+ z 3 x y z

Widać, że otrzymana nierówność jest równoważna tej, którą mieliśmy udowodnić.

Uwaga. Udowodniona przez nas nierówność, to po prostu nierówność między średnimi: arytmetyczną i harmoniczną.

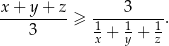
x + y+ z 3 ----------≥ 1----1---1. 3 x + y + z

Jest to szczególny przypadek ogólniejszej nierówności (jednej z tzw. nierówności Cauchy’ego), prawdziwej dla dowolnych liczb dodatnich 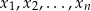x1,x 2,...,xn .

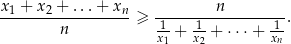
x1-+-x2-+-...+--xn ---------n-------- n ≥ 1- 1- -1 . x1 + x2 + ⋅⋅ ⋅+ xn

Łatwo tę nierówność udowodnić np. w oparciu o nierówność Jensena jak w sposobie IV.

Wersja PDF