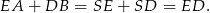Zadanie nr 1170579
Przez środek 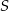 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 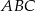 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 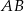 , która przecina boki
, która przecina boki 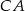 i
i 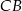 odpowiednio w punktach
odpowiednio w punktach 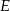 i
i 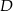 .
.
Wykaż, że 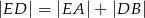 .
.
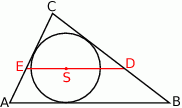
Rozwiązanie
Sposób I
Dorysujmy odcinki 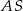 i
i 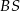 .
.
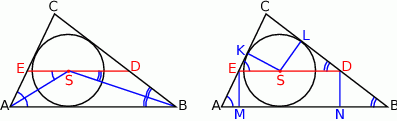
Ponieważ 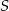 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 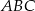 , odcinki
, odcinki 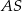 i
i 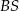 są zawarte w dwusiecznych kątów
są zawarte w dwusiecznych kątów 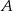 i
i 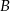 . Zatem
. Zatem 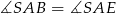 oraz
oraz 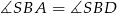 . Ponadto, z równoległości odcinków
. Ponadto, z równoległości odcinków 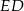 i
i 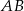 mamy
mamy
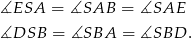
To oznacza, że trójkąty 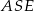 i
i 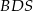 są równoramienne, czyli
są równoramienne, czyli
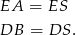
Stąd
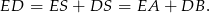
Sposób II
Tym razem niech 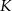 i
i 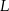 będą punktami styczności okręgu wpisanego z bokami
będą punktami styczności okręgu wpisanego z bokami 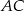 i
i 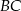 , oraz niech
, oraz niech 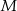 i
i 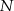 będą rzutami punktów
będą rzutami punktów 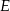 i
i 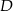 na bok
na bok 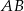 .
.
Zauważmy, że trójkąty prostokątne 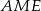 i
i 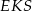 mają taki sam kąt
mają taki sam kąt 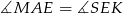 . Ponadto naprzeciw tego kąta w obu trójkątach są odcinki tej samej długości
. Ponadto naprzeciw tego kąta w obu trójkątach są odcinki tej samej długości 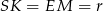 , gdzie
, gdzie  – promień okręgu wpisanego. W takim razie trójkąty te są przystające i
– promień okręgu wpisanego. W takim razie trójkąty te są przystające i 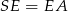 . Analogicznie uzasadniamy, że trójkąty
. Analogicznie uzasadniamy, że trójkąty 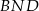 i
i 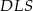 są przystające, więc
są przystające, więc 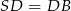 . W takim razie
. W takim razie