/Konkursy

Zadanie nr 1454077

Dodaj do ulubionych
Dodaj do rozwiązanych

Długość ramienia trapezu jest równa 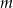m , a odległość od niego środka przeciwległego ramienia jest równa 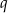q . Wyznacz pole trapezu.

Rozwiązanie

Sposób I

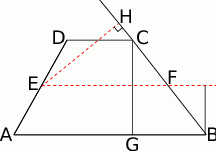
Zacznijmy od rysunku i załóżmy, że mamy dane ramię 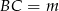BC = m .

PIC

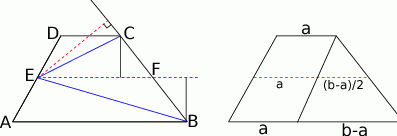
Jak się przyjrzymy, to mamy daną podstawę 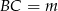BC = m i opuszczoną na nią wysokość 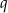q w trójkącie 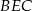BEC . Zatem pole tego trójkąta wynosi

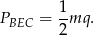
1- PBEC = 2mq .

Pokażemy, że pole tego trójkąta to dokładnie połowa pola trapezu.

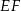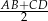Dorysujmy odcinek EF łączący środki ramion trapezu. Z twierdzenia Talesa, odcinek ten jest równoległy do podstaw, oraz z drugiego rysunku łatwo odczytać, że ma długość AB-+CD- 2 .

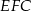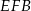Trójkąty EF C i EF B mają wspólną podstawę 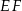EF oraz suma ich wysokości opuszczonych na tę podstawę jest równa wysokości 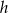h trapezu. Zatem pole trójkąta 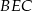BEC możemy policzyć następująco:

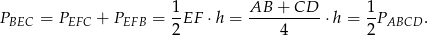
1 AB + CD 1 PBEC = PEFC + PEFB = --EF ⋅h = ----------⋅h = -PABCD . 2 4 2

Zatem pole trapezu jest równe 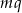mq .

Sposób II

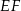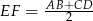Tak jak poprzednio dorysowujemy odcinek EF i zauważamy, że EF = AB-+CD- 2 .

PIC

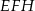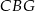Tym razem skorzystamy jednak z podobieństwa trójkątów EF H i CBG (oba są prostokątne i 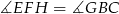∡EF H = ∡GBC ). Z tego podobieństwa mamy

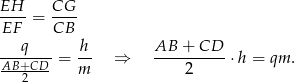
EH--= CG-- EF CB q h AB + CD AB-+CD--= m- ⇒ ----2-----⋅h = qm . 2

 
Odpowiedź: mq

Wersja PDF