Zadanie nr 1605515
Udowodnij, że jeżeli 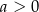 to dla wszystkich
to dla wszystkich 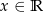 spełniona jest nierówność
spełniona jest nierówność 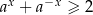 .
.
Rozwiązanie
Sposób I
Przekształćmy lewą stronę nierówności
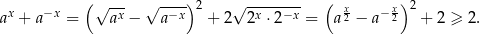
Sposób II
Jeżeli podstawimy 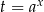 to
to 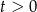 i mamy nierówność
i mamy nierówność
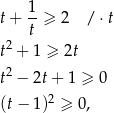
która jest oczywiście prawdziwa.
Sposób III
Niech 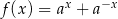 . Jeżeli
. Jeżeli 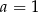 , to nierówność jest oczywiście spełniona, więc załóżmy, że
, to nierówność jest oczywiście spełniona, więc załóżmy, że 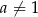 . Funkcja
. Funkcja 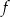 jest parzysta:
jest parzysta:
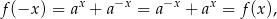
więc wystarczy udowodnić, że 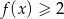 dla
dla 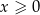 .
.
Liczymy pochodną
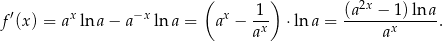
Zauważmy teraz, że jeżeli 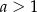 (i
(i 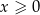 z założenia), to
z założenia), to 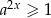 i
i 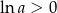 . Podobnie, jeżeli
. Podobnie, jeżeli 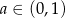 , to
, to 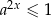 i
i 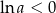 . Zatem funkcja
. Zatem funkcja 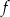 jest rosnąca na przedziale
jest rosnąca na przedziale 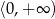 i
i
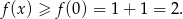
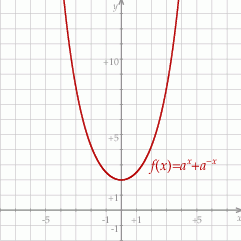
Na koniec wykres dla ciekawskich.