/Konkursy

Zadanie nr 1899474

Dodaj do ulubionych
Dodaj do rozwiązanych

Pierwsza pompa napełnia zbiornik w czasie o 15 godzin krótszym niż druga pompa. Jeżeli obie pompy pracują jednocześnie, to zbiornik zostaje napełniony w czasie 10 godzin. Ile godzin potrzeba na napełnienie zbiornika przy pomocy każdej z pomp?

Rozwiązanie

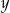Powiedzmy, że pierwsza pompa napełnia zbiornik w czasie x , a druga w czasie y godzin. W takim razie 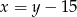x = y − 15 oraz w ciągu jednej godziny pompy, pracując razem, napełniają 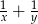1x + 1y część zbiornika. Z drugiej strony, z treści zadania wiemy, że w ciągu godziny napełniają 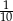-1 10 zbiornika. Mamy stąd równanie

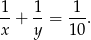
1-+ 1-= -1-. x y 10

Podstawiamy w tym równaniu 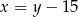x = y − 15

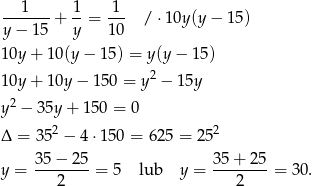
--1----+ 1-= -1- / ⋅10y (y− 15) y − 15 y 10 10y + 10(y − 15) = y(y− 15) 10y + 10y − 150 = y2 − 15y 2 y − 35y + 150 = 0 Δ = 3 52 − 4 ⋅150 = 625 = 2 52 y = 35-−-25-= 5 lub y = 35+--25-= 3 0. 2 2

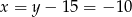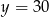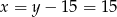Pierwsza odpowiedź daje x = y − 15 = − 10 , co nie jest możliwe. Zatem y = 30 i x = y − 15 = 15 .  
Odpowiedź: 15 i 30 godzin.

Wersja PDF