/Konkursy

Zadanie nr 2165305

Dodaj do ulubionych
Dodaj do rozwiązanych

Dwóch korektorów, pracując razem, jest w stanie dokonać poprawek w tekście w czasie 8 godzin. Jeżeli każdy z nich wykonywałby tę pracę sam, to pierwszy, bardziej doświadczony korektor zakończyłby ją o 12 godzin wcześniej niż drugi. W ciągu ilu godzin każdy z korektorów wykonałby tę pracę samodzielnie?

Rozwiązanie

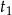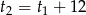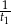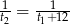Oznaczmy szukane czasy pracy korektorów przez t1 i t2 = t1 + 12 odpowiednio. Zatem w ciągu godziny wykonują oni odpowiednio t11 i -1 = --1-- t2 t1+12 część pracy. Jeżeli będą pracować razem, to w ciągu godziny wykonają

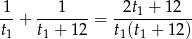
1 1 2t + 1 2 --+ ------- = ----1------ t1 t1 + 12 t1(t1 + 12)

część pracy. Całą prace wykonają w czasie

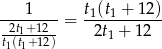
1 t (t + 12) -------- = -1--1------ t2t(t1++1122) 2t1 + 1 2 1 1

godzin. Mamy więc równanie

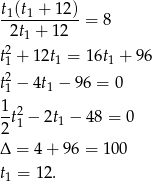
t1(t1 + 12) -----------= 8 2t1 + 12 t21 + 12t1 = 16t1 + 96 2 t1 − 4t1 − 96 = 0 1-2 2t1 − 2t1 − 4 8 = 0 Δ = 4 + 96 = 100 t1 = 1 2.

Zatem 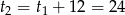t2 = t1 + 1 2 = 24 .  
Odpowiedź: 12 godzin i 24 godziny

Wersja PDF