Zadanie nr 2347157
Pięć liczb całkowitych rozmieszczono na okręgu. Okazało się, że dla każdych dwóch sąsiadujących ze sobą liczb, ani ich suma, ani suma pozostałych trzech nie jest podzielna przez 3. Ile wśród tych pięciu liczb jest podzielnych przez 3?
A) 0 B) 1 C) 2 D) 3 E) Nie można tego wyznaczyć
Rozwiązanie
Ponieważ interesuje nas podzielność przez 3, zamiast o liczbach będziemy myśleć o ich resztach z dzielenia przez 3, czyli liczbach 0,1,2. Zauważmy najpierw, że konfiguracja, gdy wszystkie liczby są równe jest zła. Podobnie, gdyby na okręgu były tylko jedynki i dwójki, to któraś jedynka musiałaby sąsiadować z dwójką i ich suma byłaby podzielna przez trzy. Musi zatem na okręgu być gdzieś 0.
Jacy są sąsiedzi 0? Nie może być zero i nie może być para 1,2 – bo wtedy suma trzech liczb dzieli się przez 3. Zatem sąsiedzi 0 to albo dwie jedynki albo dwie dwójki. Mnożąc ewentualnie wszytskie liczby na okręgu przez -1, możemy założyć, że są to dwie jedynki.
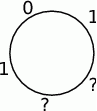
Pozostało ustalić jakie są dwie pozostałe liczby. Nie może tam być dwójki i nie mogą być dwie jedynki. Muszą to zatem być 1 i 0.
Odpowiedź: C

