/Konkursy

Zadanie nr 2350788

Dodaj do ulubionych
Dodaj do rozwiązanych

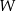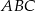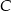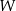Punkt W jest środkiem okręgu wpisanego w trójkąt ABC . Prosta przechodząca przez punkty C i W przecina okrąg opisany na trójkącie 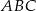ABC w punkcie 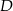D . Wykaż, że trójkąt 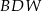BDW jest równoramienny.

Rozwiązanie

Najważniejszy jest duży rysunek.

PIC

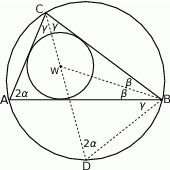
Oznaczmy 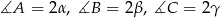∡A = 2α, ∡B = 2β , ∡C = 2γ . W szczególności

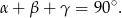
α+ β+ γ = 9 0∘.

Ponieważ punkt 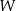W leży na przecięciu dwusiecznych, oraz korzystając z równości kątów wpisanych opartych na tym samym łuku, mamy

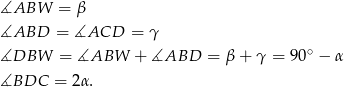
∡ABW = β ∡ABD = ∡ACD = γ ∡DBW = ∡ABW + ∡ABD = β + γ = 90∘ − α ∡BDC = 2 α.

Mamy stąd

∡DW B = 180 ∘ − (∡BDC + ∡DBW ) = 1 80∘ − (2α + 90∘ − α) = ∘ = 90 − α = ∡DBW .
Wersja PDF