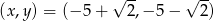/Konkursy

Zadanie nr 2398378

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż układ równań 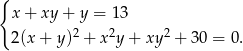{ x+ xy + y = 13 2(x+ y)2 + x2y + xy2 + 30 = 0.

Rozwiązanie

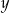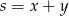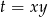Ponieważ oba równania układu są symetryczne względem x i y , możemy je zapisać używając zmiennych s = x + y i t = xy . Spróbujmy to zrobić.

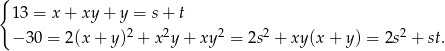
{ 13 = x+ xy + y = s + t − 30 = 2(x+ y)2 + x2y + xy2 = 2s2 + xy (x + y) = 2s2 + st.

Z pierwszego równania wyliczamy 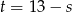t = 13 − s i podstawiamy do drugiego równania.

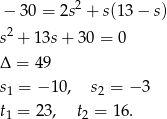
− 30 = 2s2 + s(1 3− s) 2 s + 13s + 30 = 0 Δ = 49 s1 = −1 0, s2 = − 3 t1 = 2 3, t2 = 16.

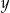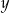Jak teraz obliczyć x i y ? Można rozwiązać odpowiedni układ równań, ale prościej jest skorzystać ze wzorów Viète’a. Liczby x i y są pierwiastkami równania

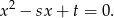
2 x − sx + t = 0.

Musimy zatem rozwiązać dwa równania

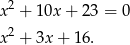
2 x + 10x + 23 = 0 x2 + 3x + 16.

Drugie z równań nie ma pierwiastków, a w przypadku pierwszego mamy 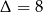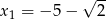Δ = 8 , √ -- x 1 = − 5− 2 i √ -- x2 = − 5 + 2 .  
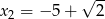Odpowiedź: 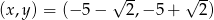√ -- √ -- (x,y) = (− 5− 2,− 5+ 2) lub √ -- √ -- (x,y ) = (− 5+ 2,− 5− 2)

Wersja PDF