Zadanie nr 2772387
Dany jest kwadrat 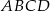 . Odcinki poprowadzone z punktów
. Odcinki poprowadzone z punktów 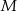 i
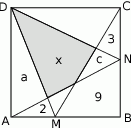
i 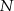 do jego wierzchołków dzielą go na osiem części. Na rysunku zaznaczono pola trzech z nich. Jakie jest pole zacieniowanej części?
do jego wierzchołków dzielą go na osiem części. Na rysunku zaznaczono pola trzech z nich. Jakie jest pole zacieniowanej części?
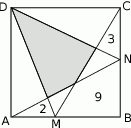
A) 14 B) 18 C) 11 D) 12 E) 9
Rozwiązanie
Oznaczmy szukane pole przez  , pola dwóch przyległych trójkątów przez
, pola dwóch przyległych trójkątów przez  i
i  – jak na rysunku, i niech połowa pola kwadratu to
– jak na rysunku, i niech połowa pola kwadratu to 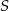 .
.
Ponieważ pole trójkata 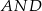 to połowa pola kwadratu to
to połowa pola kwadratu to
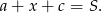
Z drugiej strony, z tego że pole trójkąta 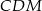 też jest równe
też jest równe 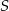 , mamy
, mamy
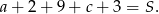
Odejmując od pierwszej równości drugą dostajemy 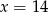 .
.
Odpowiedź: A

