Zadanie nr 2912426
Uczeń ma 2009 sześciennych klocków o krawędzi długości 1 oraz 2009 kolorowych kwadratowych naklejek o boku długości 1. Uczeń ten skleił ze wszystkich klocków prostopadłościan i okleił całą jego powierzchnię naklejkami, przyklejając dokładnie po jednej do każdej ściany klocka, tworzącej tę powierzchnię. Okazało się, że uczniowi pozostały jeszcze naklejki. Ile ich pozostało?
A) Więcej niż 1000 B) 763 C) 476 D) 49 E) Opisana sytuacja jest niemożliwa
Rozwiązanie
Ponieważ
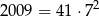
nie ma zbyt wielu możliwości sklejenia 2009 klocków w prostopadłościan.
Można zrobić prostopadłościan 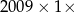 (wieża ze wszystkich klocków), ale wtedy zabraknie naklejek.
(wieża ze wszystkich klocków), ale wtedy zabraknie naklejek.
Można zrobić prostopadłościan 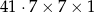 (wieża z podstawą z 7 klocków). W takim przypadku jest 2009 kwadratów w jednej ze ścian, więc też zabraknie naklejek.
(wieża z podstawą z 7 klocków). W takim przypadku jest 2009 kwadratów w jednej ze ścian, więc też zabraknie naklejek.
Ostatnia możliwość to prostopadłościan 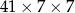 (wieża z podstawą
(wieża z podstawą 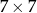 ). Policzmy liczbę kwadratów w ścianach w takiej sytuacji. Mamy
). Policzmy liczbę kwadratów w ścianach w takiej sytuacji. Mamy 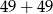 w podstawach i
w podstawach i 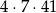 w ścianach bocznych. W sumie jest
w ścianach bocznych. W sumie jest
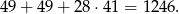
Zatem zostanie
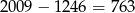
naklejek.
Odpowiedź: B

