/Konkursy

Zadanie nr 2943812

Dodaj do ulubionych
Dodaj do rozwiązanych

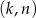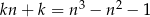Wyznacz wszystkie pary liczb całkowitych (k,n) spełniających równość kn + k = n3 − n2 − 1 .

Rozwiązanie

Przekształćmy daną równość tak, aby obliczyć 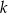k .

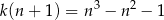
3 2 k(n+ 1) = n − n − 1

Zauważmy teraz, że jeżeli 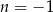n = − 1 , to otrzymujemy sprzeczność, więc możemy założyć, że 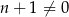n + 1 ⁄= 0 i podzielić obie strony przez n + 1 .

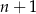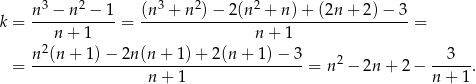
3 2 3 2 2 n-−--n-−--1- (n-+--n-)−--2(n--+-n)-+-(2n-+-2)-−-3- k = n+ 1 = n + 1 = 2 = n-(n-+-1)-−-2n(n-+--1)+-2-(n+--1)−--3-= n 2 − 2n + 2− --3--. n+ 1 n+ 1

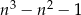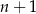To co zrobiliśmy w liczniku powyższego ułamka, to dzielenie z resztą wielomianu n3 − n2 − 1 przez n + 1 . Można to zrobić na różne sposoby, my zrobiliśmy to grupując wyrazy.

Jeżeli 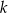k ma być liczbą całkowitą, to 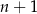n + 1 musi dzielić 3, co prowadzi do 4 możliwości:

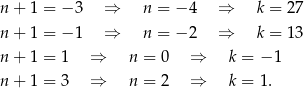
n + 1 = − 3 ⇒ n = − 4 ⇒ k = 27 n + 1 = − 1 ⇒ n = − 2 ⇒ k = 13 n + 1 = 1 ⇒ n = 0 ⇒ k = − 1 n + 1 = 3 ⇒ n = 2 ⇒ k = 1.

 
Odpowiedź: (27,− 4),(13 ,−2 ),(− 1 ,0 ),(1,2)

Wersja PDF