Zadanie nr 3256926
Wykaż, że jeżeli liczba  nie dzieli się przez 3, to liczba
nie dzieli się przez 3, to liczba 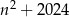 jest podzielna przez 3.
jest podzielna przez 3.
Rozwiązanie
Sposób I
Jeżeli  nie dzieli się przez 3, to możemy ją zapisać w postaci
nie dzieli się przez 3, to możemy ją zapisać w postaci 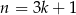 lub
lub 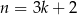 . W pierwszym przypadku
. W pierwszym przypadku
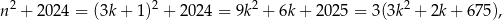
a w drugim
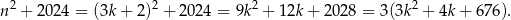
W obu przypadkach otrzymaliśmy więc liczbę podzielną przez 3.
Sposób II
Zauważmy najpierw, że
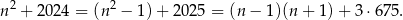
Jeżeli  nie dzieli się przez 3, to możemy ją zapisać w postaci
nie dzieli się przez 3, to możemy ją zapisać w postaci 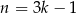 lub
lub 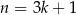 . W pierwszym przypadku mamy
. W pierwszym przypadku mamy
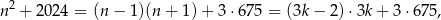
a w drugim
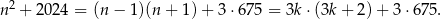
W obu przypadkach otrzymaliśmy więc liczbę podzielną przez 3.

