Zadanie nr 3455319

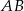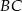Na bokach i trójkąta ostrokątnego 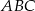ABC opisano, jako na średnicach, dwa okręgi. Gdzie leży punkt przecięcia się tych okręgów (różny od punktu B)?

Rozwiązanie

Zaczynamy od rysunku.

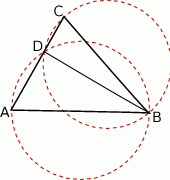
Zauważmy, że jeżeli 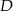jest punktem wspólnym okręgu o średnicy 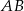i boku 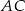(punkt taki istnieje, bo trójkąt jest ostrokątny), to 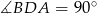∡BDA = 90∘ . Zatem 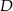jest spodkiem wysokości opuszczonej z wierzchołka 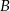na bok 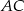. Dokładnie taką samą własność ma punkt przecięcia się okręgu opisanego na boku 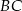i boku 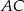. Zatem punkt 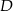, czyli spodek wysokości opuszczonej z wierzchołka 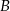, jest punktem wspólnym obu okręgów.