Zadanie nr 3479036
Andrzej, Mietek i Zbyszek rzucają kolejno kostką do gry. Andrzej wygrywa, jeżeli wyrzuci 1,2 lub 3. Mietek wygrywa, jeżeli wyrzuci 4 lub 5. Zbyszek wygrywa, jeżeli wyrzuci 6. Najpierw kostką rzuca Andrzej, potem Mietek, potem Zbyszek, potem znowu Andrzej, znowu Mietek, itd. Gra się kończy, gdy któryś z nich wygra. Jakie jest prawdopodobieństwo, że wygra Zbyszek?
A)  B)
B)  C)
C) 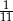 D)
D) 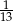 E) 0
E) 0
Rozwiązanie
Na opisaną grę należy patrzeć jak na ciąg powtarzających się cykli: rzuca Andrzej, Mietek i Zbyszek. Narysujmy sposobie pojedynczy cykl na drzewku.
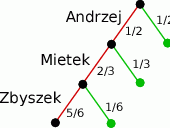
Widać z obrazka, że w danym cyklu, Zbyszek wygrywa z prawdopodobieństwem
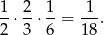
Natomiast z prawdopodobieństwem
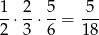
odbędzie się następna tura.
Szukane prawdopodobieństwo wynosi zatem (najlepiej wyobrazić sobie kolejne identyczne drzewka przyklejone w przegranej Zbyszka)
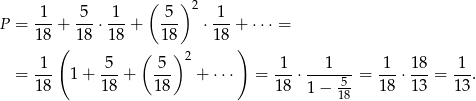
Odpowiedź: D

