Zadanie nr 3492745
Przekątne trapezu przecinają się w punkcie 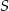 . Przez punkt
. Przez punkt 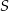 poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach
poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach 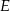 i
i 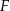 . Wykaż, że
. Wykaż, że 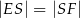 .
.
Rozwiązanie
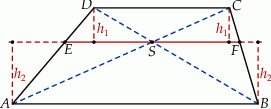
Rozpoczynamy od szkicowego rysunku.
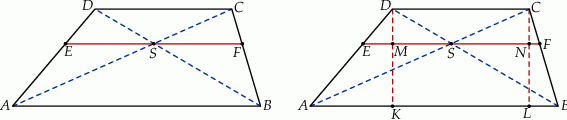
Sposób I
Zauważmy, że trójkąty 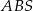 i
i 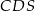 są podobne – rzeczywiście, z równoległości prostych
są podobne – rzeczywiście, z równoległości prostych 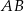 i
i 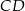 wynika, że mają one równe kąty. Oznaczmy ich skalę podobieństwa przez
wynika, że mają one równe kąty. Oznaczmy ich skalę podobieństwa przez 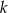 , czyli
, czyli
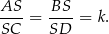
Teraz patrzymy na trójkąt 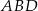 . Jest on podobny do trójkąta
. Jest on podobny do trójkąta 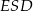 w skali
w skali
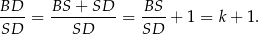
Zatem
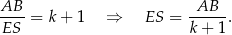
Dokładnie w ten sam sposób obliczamy długość odcinka 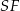 , ale tym razem patrzymy na trójkąty podobne
, ale tym razem patrzymy na trójkąty podobne 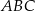 i
i 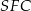 .
.
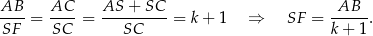
Zatem rzeczywiście
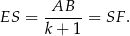
Sposób II
Dorysujmy wysokości 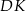 i
i 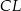 trapezu. Trójkąty
trapezu. Trójkąty 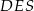 i
i 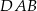 są podobne, więc
są podobne, więc
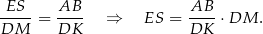
Podobnie, z podobieństwa trójkątów 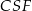 i
i 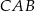 mamy
mamy
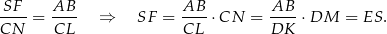
Sposób III
Patrzymy na trójkąty 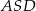 i
i 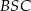 .
.
Zauważmy, że ich pola są równe, bo
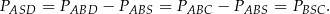
Liczymy teraz te pola w inny sposób.