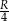/Konkursy

Zadanie nr 3569793

Dodaj do ulubionych
Dodaj do rozwiązanych

W półkole o średnicy 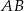AB wpisano okrąg styczny do średnicy 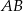AB w jej środku. Znajdź promień okręgu stycznego jednocześnie do półokręgu 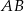AB , do wpisanego okręgu oraz do średnicy 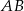AB jeżeli |AB | = 2R .

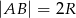Rozwiązanie

Zacznijmy od rysunku.

PIC

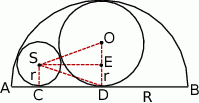
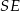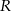Wyliczymy na dwa sposoby długość odcinka SE w zależności od promienia r mniejszego okręgu i R , co pozwoli wyliczyć r w zależności od R .

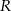Ponieważ mały okrąg i półokrąg są styczne wewnętrznie to 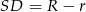SD = R − r . Z trójkąta prostokątnego 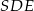SDE mamy

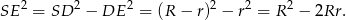
2 2 2 2 2 2 SE = SD − DE = (R − r) − r = R − 2Rr .

Z drugiej strony,

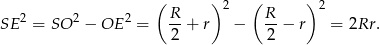
( )2 ( ) 2 SE 2 = SO 2 − OE 2 = R-+ r − R-− r = 2Rr. 2 2

Mamy zatem

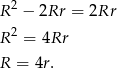
R 2 − 2Rr = 2Rr 2 R = 4Rr R = 4r.

 
Odpowiedź: R- 4

Wersja PDF