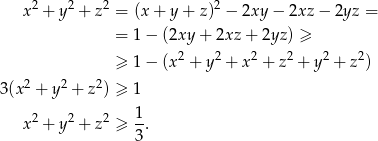Zadanie nr 3575826
Wykaż że jeżeli 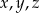 są liczbami rzeczywistymi oraz
są liczbami rzeczywistymi oraz 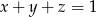 , to
, to 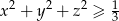 .
.
Rozwiązanie
Sposób I
Na mocy nierówności między średnią arytmetyczną i kwadratową
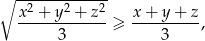
mamy
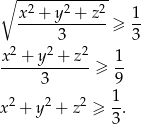
Sposób II
Skorzystamy z oczywistej nierówności
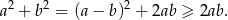
Liczymy
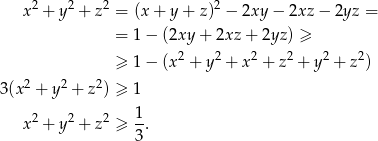
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż że jeżeli 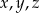 są liczbami rzeczywistymi oraz
są liczbami rzeczywistymi oraz 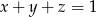 , to
, to 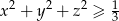 .
.
Sposób I
Na mocy nierówności między średnią arytmetyczną i kwadratową
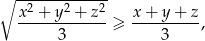
mamy
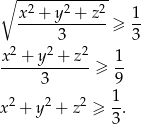
Sposób II
Skorzystamy z oczywistej nierówności
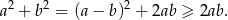
Liczymy