Zadanie nr 3788549
W matematycznej pajęczynie na rysunku obok długości wszystkich odcinków wyrażają się liczbami całkowitymi. Ile jest równe  ?
?
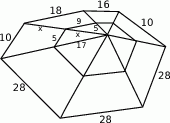
A) 11 B) 13 C) 15 D) 17 E) 19
Rozwiązanie
Najtrudniejsze w tym zadaniu jest wyeliminowanie niepotrzebnych informacji. Trochę kombinując, można zauważyć, że istotna jest tylko zewnętrzna pajęczyna – ta wewnętrzna jest po prostu dwa razy mniejsza, można na nią nie patrzeć.
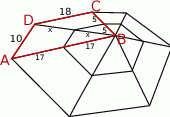
Patrząc dalej, najważniejszy jest czworokąt 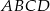 – mamy dane wszystkie jego boki, a mamy wyliczyć długość przekątnej. Oczywiście ogólnie boki czworokąta nie wyznaczają jednoznacznie długości jego przekątnej, ale my dodatkowo wiemy, że ma ona długość
– mamy dane wszystkie jego boki, a mamy wyliczyć długość przekątnej. Oczywiście ogólnie boki czworokąta nie wyznaczają jednoznacznie długości jego przekątnej, ale my dodatkowo wiemy, że ma ona długość 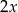 , gdzie
, gdzie  jest liczbą całkowitą. Ponadto
jest liczbą całkowitą. Ponadto 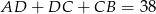 jest niewiele większe od
jest niewiele większe od 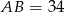 , więc wydaje się rozsądne, że punkty
, więc wydaje się rozsądne, że punkty 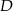 i
i 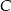 nie mają zbyt dużej swobody, to jest prawdziwy powód, dla którego uda nam się wyliczyć długość przekątnej
nie mają zbyt dużej swobody, to jest prawdziwy powód, dla którego uda nam się wyliczyć długość przekątnej 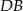 .
.
No to do dzieła, patrząc na trójąt 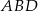 , mamy
, mamy

Z drugiej strony, z trójkąta 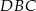 mamy
mamy

Zatem 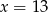 .
.
Odpowiedź: B

