/Konkursy

Zadanie nr 3847591

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że dla każdej liczby naturalnej 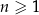n ≥ 1 liczba 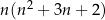2 n(n + 3n + 2) jest podzielna przez 6.

Rozwiązanie

Sposób I

Rozłóżmy trójmian, który jest nawiasie.

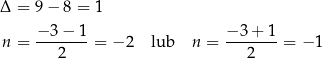
Δ = 9 − 8 = 1 −-3−--1 −-3+--1 n = 2 = − 2 lub n = 2 = − 1

W takim razie

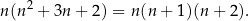
2 n(n + 3n + 2 ) = n(n + 1)(n + 2 ).

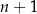Widać teraz, że liczba ta jest parzysta – bo albo n albo n + 1 jest liczbą parzystą. Podobnie, liczba ta dzieli się przez 3, bo jest to iloczyn trzech kolejnych liczb całkowitych. W takim razie całe wyrażenie zawsze dzieli się przez 2 ⋅3 = 6 .

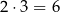Sposób II

Zauważmy najpierw, że

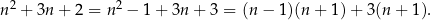
n 2 + 3n + 2 = n2 − 1 + 3n + 3 = (n − 1)(n+ 1)+ 3(n + 1).

Stąd

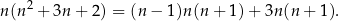
n(n2 + 3n + 2) = (n − 1)n(n + 1) + 3n (n+ 1).

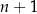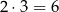Zauważmy teraz, że oba składniki tej sumy są parzyste – bo albo n albo n + 1 jest liczbą parzystą. Oba tez dzielą się przez 3 – jest to oczywiste dla drugiego składnika, a pierwszy składnik to iloczyn trzech kolejnych liczb całkowitych, więc jedna z nich dzieli się przez 3. W takim razie całe wyrażenie zawsze dzieli się przez 2 ⋅3 = 6 .

Wersja PDF