/Konkursy

Zadanie nr 3942779

Dodaj do ulubionych
Dodaj do rozwiązanych

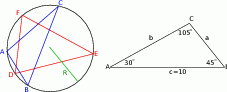
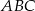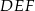Trójkąty ABC i DEF wpisano w ten sam okrąg. Udowodnij, że równość obwodów tych trójkątów jest równoważna równości sum sinusów ich kątów wewnętrznych.

Rozwiązanie

Żeby móc w miarę wygodnie zapisać rozwiązanie, przyjmijmy, że małe litery 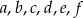a,b,c,d,e,f oznaczają długości boków leżących naprzeciw kątów 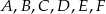A ,B ,C ,D ,E,F w odpowiednich trójkątach.

PIC

Z twierdzenia sinusów

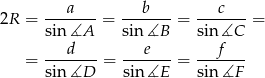
2R = ---a--- = ---b--- = ---c---= sin∡A sin ∡B sin ∡C ---d--- --e---- --f---- = sin∡D = sin ∡E = sin ∡F

Mamy stąd

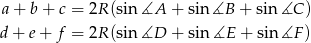
a+ b+ c = 2R (sin ∡A + sin ∡B + sin ∡C ) d+ e+ f = 2R (sin ∡D + sin ∡E + sin ∡F )

co łatwo prowadzi do żądanej równoważności.

Wersja PDF