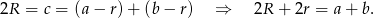Zadanie nr 4330397
Wykaż, że w trójkącie prostokątnym suma długości obu przyprostokątnych jest równa sumie długości średnic okręgów wpisanego i opisanego na tym trójkącie.
Rozwiązanie
Jeżeli przyprostokątne trójkąta to  i
i 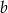 , a przeciwprostokątna
, a przeciwprostokątna  , to mamy
, to mamy 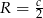 , bo średnicą okręgu opisanego na trójkącie prostokątnym jest dokładnie przeciwprostokątna.
, bo średnicą okręgu opisanego na trójkącie prostokątnym jest dokładnie przeciwprostokątna.
Sposób I
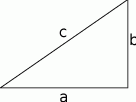
Promień  okręgu wpisanego możemy wyliczyć ze wzoru na pole
okręgu wpisanego możemy wyliczyć ze wzoru na pole
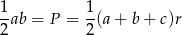
Mamy zatem
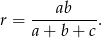
Liczymy sumę średnic
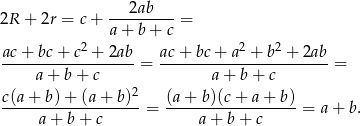
Sposób II
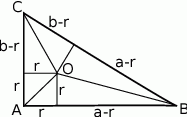
Jeżeli połączymy środek 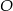 okręgu wpisanego w trójkąt prostokątny
okręgu wpisanego w trójkąt prostokątny 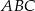 z jego wierzchołkami, to odcinki te dzielą kąty trójkąta na połowy. Jeżeli dorysujemy jeszcze rzuty punktu
z jego wierzchołkami, to odcinki te dzielą kąty trójkąta na połowy. Jeżeli dorysujemy jeszcze rzuty punktu 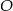 na boki trójkąta, to mamy trzy pary przystających trójkątów prostokątnych. Oznaczając odpowiednio ich boki, widać, że
na boki trójkąta, to mamy trzy pary przystających trójkątów prostokątnych. Oznaczając odpowiednio ich boki, widać, że