Zadanie nr 4787693
Okrąg wpisany w trójkąt prostokątny 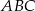 o bokach długości
o bokach długości 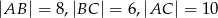 jest styczny do boków
jest styczny do boków 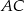 i
i 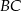 w punktach
w punktach 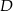 i
i 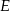 . Proste
. Proste 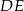 i
i 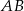 przecinają się punkcie
przecinają się punkcie 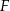 . Oblicz pole trójkąta
. Oblicz pole trójkąta 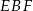 .
.
Rozwiązanie
Rozpoczynamy oczywiście od rysunku.
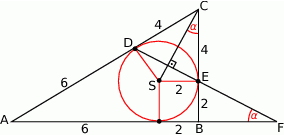
Zacznijmy od wyliczenia promienia okręgu wpisanego w trójkąt 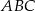 . Ze wzoru na pole z promieniem okręgu wpisanego mamy
. Ze wzoru na pole z promieniem okręgu wpisanego mamy
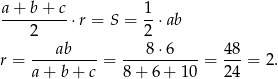
Zatem 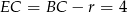 .
.
Na narysowanym obrazku jest sporo trójkątów prostokątnych – w tym interesujący nas trójkąt 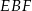 . Kluczowe do rozwiązania zadania jest zauważenie, że niektóre z nich są podobne. Rzeczywiście, jeżeli oznaczymy
. Kluczowe do rozwiązania zadania jest zauważenie, że niektóre z nich są podobne. Rzeczywiście, jeżeli oznaczymy 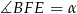 to
to
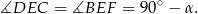
Stąd
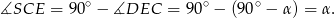
To oznacza, że trójkąty 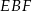 i
i 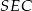 są podobne. W obu z nich długość przyprostokątnej leżącej naprzeciw kąta
są podobne. W obu z nich długość przyprostokątnej leżącej naprzeciw kąta  jest równa 2, więc trójkąty te są przystające. Zatem
jest równa 2, więc trójkąty te są przystające. Zatem 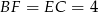 i interesujące nas pole jest równe
i interesujące nas pole jest równe
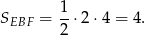
Odpowiedź: 4

