/Konkursy

Zadanie nr 4823413

Dodaj do ulubionych
Dodaj do rozwiązanych

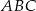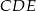Trójkąty równoboczne ABC i CDE są położone tak, jak na poniższym rysunku. Wykaż, że |AD | = |BE | .

PIC

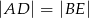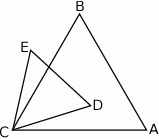
Rozwiązanie

Dorysujmy odcinki 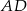AD i BE .

PIC

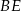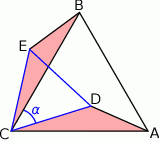
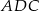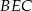Patrzymy teraz na trójkąty ADC i BEC . Mają one dwie pary równych boków

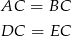
AC = BC DC = EC

oraz równy kąt przy wierzchołku 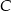C

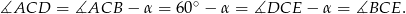
∘ ∡ACD = ∡ACB − α = 60 − α = ∡DCE − α = ∡BCE .

Trójkąty te są więc przystające, czyli 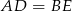AD = BE .

Wersja PDF