/Konkursy
LX Olimpiada Matematyczna I stopień 2008/2009
I seria
Na niektórych polach szachownicy rozmiaru 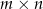 ustawiono wieże. Wiadomo, że dowolna wieża znajduje się w polu rażenia co najwyżej dwóch innych wież. Wyznaczyć, w zależności od
ustawiono wieże. Wiadomo, że dowolna wieża znajduje się w polu rażenia co najwyżej dwóch innych wież. Wyznaczyć, w zależności od  , największą liczbę wież na szachownicy, dla której taka sytuacja jest możliwa.
, największą liczbę wież na szachownicy, dla której taka sytuacja jest możliwa.
Oczywiście zaczynamy od prób i po jakimś czasie można wymyślić, że da się ustawić 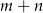 wież. Przykład takiego ustawienia na rysunku.
wież. Przykład takiego ustawienia na rysunku.
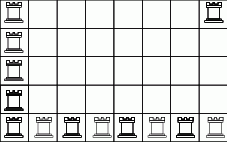
Spróbujemy pokazać, że więcej wież postawić się nie da.
Sposób I
Przypuśćmy, że na szachownicy da się ustawić  wież tak, aby każda znajdowała się w polu rażenia co najwyżej dwóch. Dodatkowo przyjmijmy, że
wież tak, aby każda znajdowała się w polu rażenia co najwyżej dwóch. Dodatkowo przyjmijmy, że 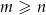 i
i 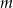 jest liczbą wierszy. Gdyby w każdej kolumnie były co najwyżej 2 wieże to wszystich wież byłoby co najwyżej
jest liczbą wierszy. Gdyby w każdej kolumnie były co najwyżej 2 wieże to wszystich wież byłoby co najwyżej 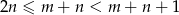 . Zatem w pewnej kolumnie muszą być co najmniej 3 wieże.
. Zatem w pewnej kolumnie muszą być co najmniej 3 wieże.

Spośród tych wież wybierzmy środkową – jest ona atakowana przez dwie wieże, zatem odpowiadający jej wiersz nie może zawierać żadnych innych wież. Usuwamy ten wiersz i mamy poprawną sytuację w tablicy rozmiaru 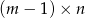 i w której jest
i w której jest  wież. To jest nasz krok indukcyjny. Kontynuujemy tę operację aż dojdziemy do tablicy
wież. To jest nasz krok indukcyjny. Kontynuujemy tę operację aż dojdziemy do tablicy  , na której jest
, na której jest
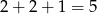
wież. Oczywiście jest to niemożliwe.
Sposób II
Zauważmy, że z warunków zadania wynika, że każda wieża „widzi" co najmniej dwie krawędzie brzegowych pól szachownicy (bo najwyżej dwa ma zasłonięte). Wszystkich takich krawędzi pól jest 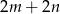 , zatem wszystkich wież nie może być więcej niż
, zatem wszystkich wież nie może być więcej niż 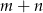 (bo każde pole brzegowe może widzeć tylko jedna wieża).
(bo każde pole brzegowe może widzeć tylko jedna wieża).
Odpowiedź: 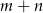
Dana jest liczba całkowita 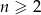 . Niech
. Niech 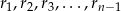 będą odpowiednio resztami z dzielenia liczb
będą odpowiednio resztami z dzielenia liczb
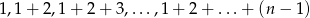
przez  . Znaleźć wszystkie takie wartości
. Znaleźć wszystkie takie wartości  , że ciąg
, że ciąg 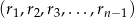 jest permutacją ciągu
jest permutacją ciągu  .
.
Dla prostoty nie będziemy odróżniać ciągu
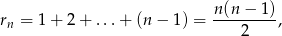
od ciągu reszt jakie dają te liczby przy dzieleniu przez  (
( będziemy mieli cały czas ustalone, więc nie prowadzi to do nieporozumień).
będziemy mieli cały czas ustalone, więc nie prowadzi to do nieporozumień).
Po pierwsze wypisujemy sobie pierwszych kilka (kilkanaście) początkowych wyrazów ciągu 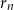 i patrzymy dla jakich
i patrzymy dla jakich  ciągi reszt są takie jak powinny być. Jak się to zrobi to narzuca się odpowiedź – będzie OK tylko dla potęg 2, czyli liczb postaci
ciągi reszt są takie jak powinny być. Jak się to zrobi to narzuca się odpowiedź – będzie OK tylko dla potęg 2, czyli liczb postaci 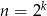 . Ponadto dla liczb nieparzystych ostatnia reszta
. Ponadto dla liczb nieparzystych ostatnia reszta  dzieli się przez
dzieli się przez  . Spróbujmy to uzasadnić.
. Spróbujmy to uzasadnić.
Jeżeli 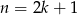 jest nieparzyste to sprawa jest prosta
jest nieparzyste to sprawa jest prosta
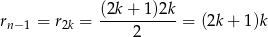
i widać, że liczba ta jest podzielna przez  (a więc nie należy do zbioru
(a więc nie należy do zbioru 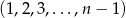 )
)
O zadaniu trzeba myśleć następująco: ciąg reszt będzie żądaną permutacją, jeżeli każde dwie reszty będą różne. Aby tak było wystarczy, że 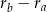 nie dzieli się przez
nie dzieli się przez  dla
dla 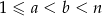 . Ze wzoru na sumę ciągu arytmetycznego mamy
. Ze wzoru na sumę ciągu arytmetycznego mamy

Załóżmy najpierw, że  ma czynnik nieparzysty, czyli jest postaci
ma czynnik nieparzysty, czyli jest postaci  i
i 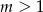 . Spróbujmy dobrać
. Spróbujmy dobrać  i
i 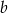 , żeby różnica reszt wyszła podzielna przez
, żeby różnica reszt wyszła podzielna przez  . Trochę kombinując, można to wymyślić:
. Trochę kombinując, można to wymyślić:
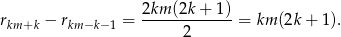
W powyższej równości jest jeden drobny detal, mianowicie dla 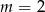 i
i 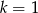 mamy
mamy 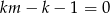 , ale przypadek
, ale przypadek 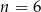 możemy rozważyć osobno (lub przyjąć, że
możemy rozważyć osobno (lub przyjąć, że  ).
).
Pozostało zastanowić się nad przypadkiem  . Zastanówmy się czy liczba
. Zastanówmy się czy liczba
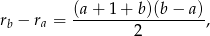
gdzie 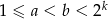 , może dzielić się przez
, może dzielić się przez 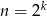 . Zauważmy, że tylko jedna z liczb
. Zauważmy, że tylko jedna z liczb 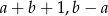 jest parzysta i w dodatku maksymalnie może dzielić się przez
jest parzysta i w dodatku maksymalnie może dzielić się przez 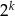 (bo obie liczby są mniejsze od
(bo obie liczby są mniejsze od 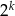 , więc oba wyrażenia są mniejsze od
, więc oba wyrażenia są mniejsze od 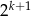 ). Zatem liczba
). Zatem liczba
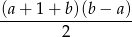
nie dzieli się przez potęgę 2 wyższą niż 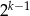 , co kończy dowód.
, co kończy dowód.
Okrąg wpisany w trójkąt 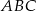 jest styczny do boków
jest styczny do boków 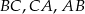 odpowiednio w punktach
odpowiednio w punktach 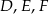 . Punkty
. Punkty 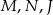 są odpo- wiednio środkami okręgów wpisanych w trójkąty
są odpo- wiednio środkami okręgów wpisanych w trójkąty 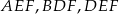 . Dowieść, że punkty
. Dowieść, że punkty 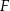 i
i 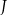 są symetryczne względem prostej
są symetryczne względem prostej 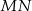 .
.
W tym zadaniu (jak to często w geometrii) najważniejszy jest rysunek – to on powie nam co mamy robić.
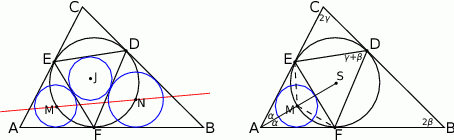
Gdy dokładnie narysujemy opisaną sytuację, to pierwsza rzecz która się narzuca, to że punkty 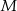 i
i 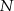 leżą na okręgu wpisanym w trójkąt
leżą na okręgu wpisanym w trójkąt 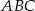 . Zanim zaczniemy kombinować do czego to się może przydać, spróbujmy sprawdzić czy tak jest (prawy rysunek).
. Zanim zaczniemy kombinować do czego to się może przydać, spróbujmy sprawdzić czy tak jest (prawy rysunek).
To co musimy sprawdzić, to czy 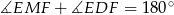 (bo to jest warunek na to, aby punkt
(bo to jest warunek na to, aby punkt 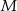 leżał na okręgu opisanym na trójkącie
leżał na okręgu opisanym na trójkącie 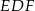 , albo jak ktoś woli na to, żeby na czworokącie
, albo jak ktoś woli na to, żeby na czworokącie 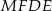 można było opisać okrąg). Oba kąty łatwo jest wyliczyć korzystając z tego, że trójkąty
można było opisać okrąg). Oba kąty łatwo jest wyliczyć korzystając z tego, że trójkąty  są równoramienne. Jeżeli oznaczymy kąty jak na rysunku to mamy
są równoramienne. Jeżeli oznaczymy kąty jak na rysunku to mamy
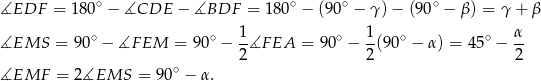
Jest więc jasne, że 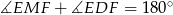 , czyli punkt
, czyli punkt 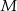 leży na okręgu wpisanym w trójkąt
leży na okręgu wpisanym w trójkąt  . Oczywiście podobnie jest z punktem
. Oczywiście podobnie jest z punktem 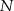 . Zanim przejdziemy dalej, zauważmy jeszcze, że punkt
. Zanim przejdziemy dalej, zauważmy jeszcze, że punkt 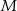 dzieli łuk
dzieli łuk 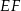 na połowy, a punkt
na połowy, a punkt 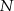 dzieli na połowy łuk
dzieli na połowy łuk 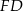 .
.
Ok, teraz z powrotem popatrzmy na wyjściowy obrazek i się zastanówmy co dalej robić.
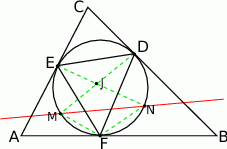
Ponieważ punkt  dzieli łuk
dzieli łuk  na połowy, prosta
na połowy, prosta  jest dwusieczną kąta
jest dwusieczną kąta  . Zatem leży na niej punkt
. Zatem leży na niej punkt  . Podobnie, punkty
. Podobnie, punkty 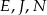 są współliniowe. Ponadto, z tych samych powodów, prosta
są współliniowe. Ponadto, z tych samych powodów, prosta 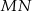 jest dwusieczną kąta
jest dwusieczną kąta 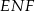 oraz kąta
oraz kąta 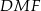 . Zatem czworokąt
. Zatem czworokąt 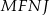 musi być deltoidem, co dowodzi, że punkty
musi być deltoidem, co dowodzi, że punkty 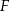 i
i 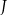 są symetryczne względem prostej
są symetryczne względem prostej 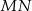 .
.
Udowodnić, że dla dowolnych nieujemnych liczb rzeczywistych 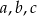 prawdziwa jest nierówność
prawdziwa jest nierówność
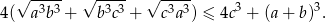
Sposób I
Spróbujemy przkształcić podaną nierówność zwijając do pełnego kwadratu.
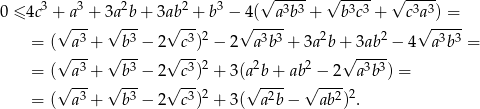
Jest jasne, że nierówność ta jest zawsze spełniona.
Sposób II
Ponieważ nierówność jest jednorodna (stopień każdego jednomianu to 3), więc łatwo możemy pozbyć się jednej niewiadomej, powiedzmy  , dzieląc przez
, dzieląc przez 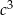 .
.
Osobno rozważmy najpierw przypadek 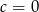 .
.
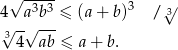
Nierówność ta łatwo wynika z nierówności między średnimi 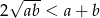 .
.
Jeżeli 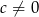 , to podzielmy obie strony przez
, to podzielmy obie strony przez 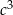 .
.
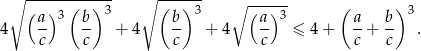
Podstawiamy teraz 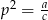 i
i 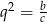 i mamy
i mamy
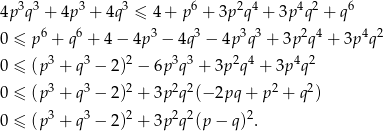
Twoje uwagi
W rozwiązaniach jest błąd lub literówka?
Masz inny pomysł na rozwiązanie zadania?
Napisz nam o tym!

