/Konkursy

Zadanie nr 5264862

Dodaj do ulubionych
Dodaj do rozwiązanych

Wartość sumy 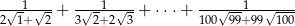---1---- ----1--- ------1------- 2√1+√ 2 + 3√2+ 2√3 + ⋅⋅⋅+ 100√99+99√100 jest równa
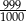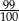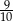A) -999- 1000 B) -99 100 C) 9- 10 D) 9 E) 1

Rozwiązanie

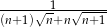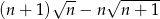Jak zwykle w tego typu zadaniach, musimy zapisać ułamek -------1------- (n+ 1)√n +n√n-+1- jako różnicę dwóch ułamków (żeby w sumie się poskracały). Zasadniczy problem polega na skomplikowanej postaci mianownika – przede wszystkim przez pierwiastki. Zacznijmy więc od ich usunięcia – mnożymy licznik i mianownik przez √ -- √ ------ (n+ 1) n − n n + 1 .

√ -- √ ------ -------√---1---√-------= (n-+-1)--n-−-n---n+--1-= (n + 1 ) n− n n + 1 (n + 1)2n + n 2(n+ 1) √ -- √ ------ √ -- √ ------ = (n-+--1)--n−--n--n-+-1-= (n-+-1)--n-−-n---n-+-1-= (n + 1)n[n + 1 − n] n(n + 1) √ -- √ ------ = --n-− --n-+-1-. n n + 1

Szukana suma jest więc równa

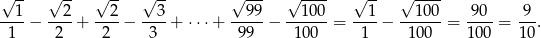
√ -- √ -- √ -- √ -- √ --- √ ---- √ -- √ ---- --1-− --2+ --2-− ---3+ ⋅⋅⋅+ --99-− --10-0 = --1-− --100-= 9-0-= 9-. 1 2 2 3 99 10 0 1 100 100 10

 
Odpowiedź: C

Wersja PDF