Zadanie nr 5266395
Dane są dwa półokręgi o wspólnym środku 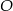 i średnicach odpowiednio
i średnicach odpowiednio 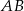 i
i 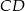 (punkty
(punkty 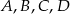 i
i 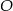 są współliniowe).
są współliniowe).
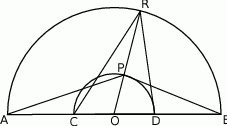
Punkt 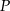 leży na wewnętrznym półokręgu, punkt
leży na wewnętrznym półokręgu, punkt 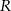 leży na zewnętrznym półokręgu, punkty
leży na zewnętrznym półokręgu, punkty 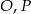 i
i 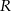 są współliniowe. Udowodnij, że
są współliniowe. Udowodnij, że 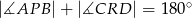 .
.
Rozwiązanie
Zauważmy, że trójkąty 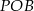 i
i 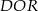 są przystające. Rzeczywiście, mamy
są przystające. Rzeczywiście, mamy 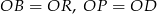 oraz boki te tworzą wspólny kąt
oraz boki te tworzą wspólny kąt 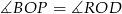 .
.
Podobnie uzasadniamy, że przystające są trójkąty 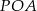 i
i 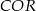 .
.
Mamy więc
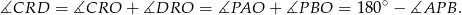
W ostatniej równości skorzystaliśmy z sumy kątów w trójkącie 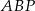 .
.

