Zadanie nr 5567063
Trójkąt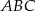 
jest podstawą ostrosłupa 
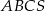. Punkt 
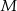jest środkiem boku 
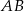i 
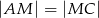. Odcinek 
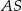jest wysokością tego ostrosłupa. Wykaż, że kąt 
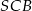jest prosty.
Rozwiązanie
W rozwiązaniu tego zadania najważniejsze są: wyraźny rysunek i odrobina wyobraźni.
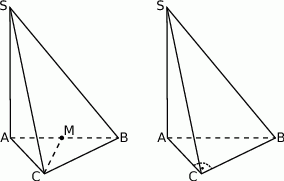
Zacznijmy od punktu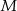 
. Z podanych informacji wynika, że jest on środkiem okręgu opisanego na trójkącie 
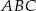(bo jest równoodległy od wszystkich trzech wierzchołków). W takim razie odcinek 
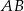jest średnicą tego okręgu, czyli kąt 
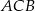jest oparty na średnicy, czyli prosty. Zapamiętajmy zatem, że 
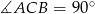i możemy zapomnieć o punkcie 
.
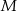Ponieważ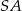 
jest wysokością ostrosłupa, płaszczyzny 
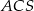i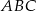 
są do siebie prostopadłe. Ponadto, jak już zauważyliśmy, odcinek 
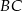jest prostopadły do krawędzi wspólnej tych płaszczyzn, czyli do 
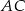. To oznacza, że odcinek ten jest prostopadły do płaszczyzny 
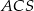. W takim razie jest on prostopadły do każdej prostej zawartej w tej płaszczyźnie, w szczególności jest prostopadły do 
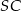. Zatem 
.
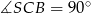