/Konkursy

Zadanie nr 5708633

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że jeżeli długości 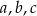a ,b,c boków trójkąta spełniają równość

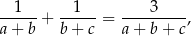
1 1 3 ------+ ----- = ---------, a+ b b + c a+ b+ c

to promień okręgu opisanego na tym trójkącie jest równy 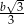b√3- 3 .

Rozwiązanie

Szkicujemy trójkąt.

PIC

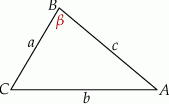
Przekształcamy daną równość.

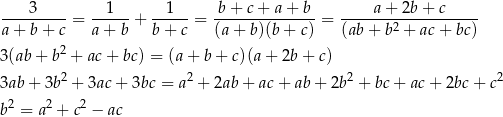
---3-----= --1---+ --1-- = b-+-c-+-a-+-b-= -----a+--2b+--c---- a+ b + c a + b b + c (a+ b)(b+ c) (ab + b2 + ac + bc) 3(ab + b 2 + ac + bc) = (a + b + c)(a + 2b + c) 3ab + 3b 2 + 3ac + 3bc = a2 + 2ab + ac+ ab+ 2b2 + bc+ ac+ 2bc+ c2 2 2 2 b = a + c − ac

Wyrażenie, które otrzymaliśmy bardzo przypomina twierdzenie cosinusów:

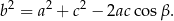
b2 = a2 + c2 − 2acco sβ.

Jeżeli porównamy prawe strony tych równości, to otrzymamy 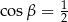co sβ = 1 2 , czyli 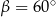∘ β = 60 . Pozostało teraz skorzystać z twierdzenia sinusów

b b b 2b 2R = -----= ------∘ = -√- = √--- sin β sin6 0 23- 3 √ -- R = √b--= b--3. 3 3
Wersja PDF