Zadanie nr 5734638
Wewnątrz trójąta 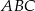 obrano punkt
obrano punkt 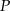 odległy od prostych
odległy od prostych 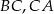 i
i 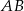 odpowiednio o
odpowiednio o 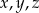 . Wykaż że
. Wykaż że
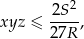
gdzie 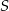 jest polem trójkąta, a
jest polem trójkąta, a 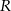 promieniem okręgu opisanego. Dla jakich punktów
promieniem okręgu opisanego. Dla jakich punktów 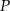 zachodzi równość?
zachodzi równość?
Rozwiązanie
Zaczynamy od rysunku.
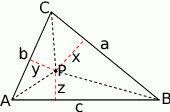
Jaki jest związek między długościami 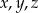 a polem trójkąta? – to łatwe, trójkąt
a polem trójkąta? – to łatwe, trójkąt 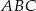 jest sumą trójkątów
jest sumą trójkątów 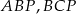 i
i 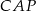 , więc
, więc
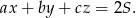
Jak to zamienić na iloczyn 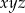 ? – stosujemy nierówność między średnimi.
? – stosujemy nierówność między średnimi.
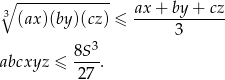
Teraz pozostało skorzystać ze wzoru na pole 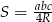 .
.
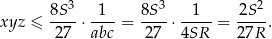
Kiedy w tej nierówności zajdzie równość? – równość w nierówności między średnimi zachodzi, gdy wszystkie liczby są równe, czyli dla 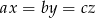 . Geometrycznie oznacza to, że pola trzech trójkątów
. Geometrycznie oznacza to, że pola trzech trójkątów 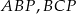 i
i 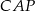 są równe.
są równe.

