/Konkursy

Zadanie nr 5827435

Dodaj do ulubionych
Dodaj do rozwiązanych

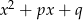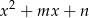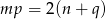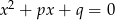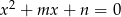Wykaż, że jeżeli między współczynnikami trójmianów 2 x + px + q i x 2 + mx + n zachodzi związek mp = 2(n + q ) , to przynajmniej jedno z równań x 2 + px + q = 0 lub x2 + mx + n = 0 ma rozwiązanie.

Rozwiązanie

Gdyby żadne z tych równań nie miało rozwiązania, to mielibyśmy nierówności

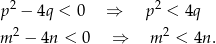
2 2 p − 4q < 0 ⇒ p < 4q m 2 − 4n < 0 ⇒ m 2 < 4n.

Jeżeli dodamy te nierówności stronami (robimy to, żeby jakoś wykorzystać podany warunek 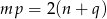mp = 2 (n+ q) – w tym warunku występują jednocześnie parametry z obu równań) i skorzystamy z równości 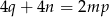4q + 4n = 2mp , to mamy

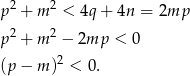
2 2 p + m < 4q + 4n = 2mp p2 + m 2 − 2mp < 0 (p − m )2 < 0.

Otrzymana nierówność jest oczywiście sprzeczna, co oznacza, że nasze założenie, że żadne z równań nie ma pierwiastków musiało być błędne.

Wersja PDF