/Konkursy

Zadanie nr 5927911

Dodaj do ulubionych
Dodaj do rozwiązanych

Trzy okręgi o promieniach 2, 4 i 6 są parami zewnętrznie styczne. Oblicz długość promienia okręgu zawierającego punkty styczności tych okręgów.

Rozwiązanie

Zacznijmy od rysunku

PIC

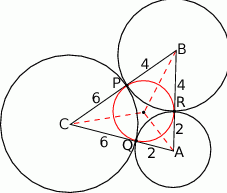
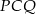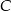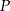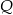Ponieważ trójkąt P CQ jest równoramienny, środek szukanego okręgu będzie leżał na dwusiecznej kąta C (bo ma być jednakowo odległy od P i Q ), podobnie uzasadniamy, że środek ten leży na pozostałych dwusiecznych trójkąta 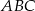ABC . Zatem okrąg przechodzący przez punkty 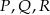P,Q ,R jest okręgiem wpisanym w trójkąt 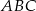ABC . Jego promień możemy wyliczyć ze wzoru na pole 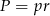P = pr , gdzie

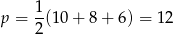
p = 1(10 + 8 + 6) = 12 2

jest połową obwodu trójkąta.

Sposób I

Pole możemy wyliczyć ze wzoru Herona

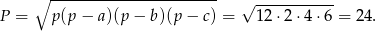
∘ ----------------------- √ ----------- P = p (p − a)(p− b)(p − c) = 12 ⋅2 ⋅4⋅ 6 = 24.

Zatem szukany promień jest równy

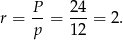
r = P-= 24-= 2. p 12

Sposób II

Pole możemy wyliczyć odrobinę prościej, jeżeli zauważymy, że trójkąt 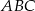ABC ma boki długości 6,10,8, czyli jest prostokątny (bo 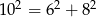10 2 = 62 + 82 ). Zatem jego pole jest równe

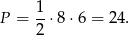
1- P = 2 ⋅8 ⋅6 = 24.

Promień liczymy jak w poprzednim sposobie.  
Odpowiedź: 2

Wersja PDF