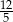Zadanie nr 7509557
Przez wierzchołek kąta prostego trójkąta prostokątnego o przyprostokątnych 8 i 15 poprowadzono prostą, która dzieli ten trójkąt na dwa trójkąty o równych obwodach. Znajdź stosunek promieni okręgów wpisanych w otrzymane z podziału trójkąty.
Rozwiązanie
Zaczynamy od rysunku.
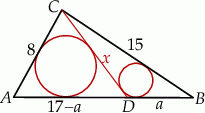
Spróbujmy na początek ustalić na jakie odcinki dzieli przeciwprostokątną poprowadzona prosta. Jeżeli oznaczymy 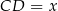 i
i 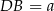 , to z równości obwodów trójkątów
, to z równości obwodów trójkątów 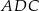 i
i 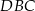 mamy
mamy

Jeżeli oznaczymy ten wspólny obwód trójkątów 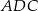 i
i 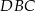 przez
przez 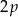 , to promienie okręgów wpisanych możemy obliczyć ze wzoru na pole
, to promienie okręgów wpisanych możemy obliczyć ze wzoru na pole 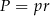 .
.
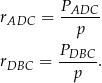
Zatem szukany iloraz wynosi
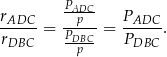
Ponieważ trójkąty 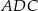 i
i 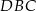 mają wspólną wysokość opuszczoną z wierzchołka
mają wspólną wysokość opuszczoną z wierzchołka 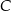 , stosunek ich pól, to dokładnie stosunek ich podstaw.
, stosunek ich pól, to dokładnie stosunek ich podstaw.
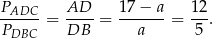
Odpowiedź: