Zadanie nr 8671292
Na niektórych polach szachownicy rozmiaru 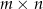 ustawiono wieże. Wiadomo, że dowolna wieża znajduje się w polu rażenia co najwyżej dwóch innych wież. Wyznaczyć, w zależności od
ustawiono wieże. Wiadomo, że dowolna wieża znajduje się w polu rażenia co najwyżej dwóch innych wież. Wyznaczyć, w zależności od 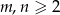 , największą liczbę wież na szachownicy, dla której taka sytuacja jest możliwa.
, największą liczbę wież na szachownicy, dla której taka sytuacja jest możliwa.
Rozwiązanie
Oczywiście zaczynamy od prób i po jakimś czasie można wymyślić, że da się ustawić 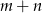 wież. Przykład takiego ustawienia na rysunku.
wież. Przykład takiego ustawienia na rysunku.
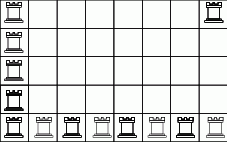
Spróbujemy pokazać, że więcej wież postawić się nie da.
Sposób I
Przypuśćmy, że na szachownicy da się ustawić  wież tak, aby każda znajdowała się w polu rażenia co najwyżej dwóch. Dodatkowo przyjmijmy, że
wież tak, aby każda znajdowała się w polu rażenia co najwyżej dwóch. Dodatkowo przyjmijmy, że 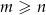 i
i 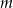 jest liczbą wierszy. Gdyby w każdej kolumnie były co najwyżej 2 wieże to wszystich wież byłoby co najwyżej
jest liczbą wierszy. Gdyby w każdej kolumnie były co najwyżej 2 wieże to wszystich wież byłoby co najwyżej 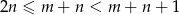 . Zatem w pewnej kolumnie muszą być co najmniej 3 wieże.
. Zatem w pewnej kolumnie muszą być co najmniej 3 wieże.

Spośród tych wież wybierzmy środkową – jest ona atakowana przez dwie wieże, zatem odpowiadający jej wiersz nie może zawierać żadnych innych wież. Usuwamy ten wiersz i mamy poprawną sytuację w tablicy rozmiaru 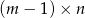 i w której jest
i w której jest 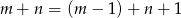 wież. To jest nasz krok indukcyjny. Kontynuujemy tę operację aż dojdziemy do tablicy
wież. To jest nasz krok indukcyjny. Kontynuujemy tę operację aż dojdziemy do tablicy 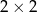 , na której jest
, na której jest
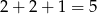
wież. Oczywiście jest to niemożliwe.
Sposób II
Zauważmy, że z warunków zadania wynika, że każda wieża „widzi" co najmniej dwie krawędzie brzegowych pól szachownicy (bo najwyżej dwa ma zasłonięte). Wszystkich takich krawędzi pól jest 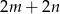 , zatem wszystkich wież nie może być więcej niż
, zatem wszystkich wież nie może być więcej niż 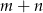 (bo każde pole brzegowe może widzeć tylko jedna wieża).
(bo każde pole brzegowe może widzeć tylko jedna wieża).
Odpowiedź: