/Konkursy

Zadanie nr 8710765

Dodaj do ulubionych
Dodaj do rozwiązanych

Basen można napełnić, otwierając zawór nr 1, a opróżnić, odkręcając zawór nr 2. Jeśli otworzony jest tylko jeden zawór, całkowite napełnienie basenu trwa o godzinę krócej niż jego opróżnienie. Gdy równocześnie odkręcono obydwa zawory, basen napełnił się w ciągu 12 godzin. W ciągu ilu godzin napełni się basen, jeżeli zawór nr 2 będzie zamknięty?

Rozwiązanie

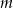Powiedzmy, że zawór nr 1 napełnia basen w ciągu n godzin, a zawór nr 2 opróżnia basen w ciągu m godzin. W takim razie w ciągu jednej godziny zawór nr 1 napełnia 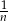1n , a zawór nr 2 opróżnia 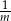m1 część basenu. Z podanych informacji otrzymujemy więc układ równań.

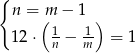
{ n = m − 1 ( 1 1 ) 12 ⋅ n − m- = 1

Podstawiamy 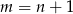m = n + 1 z pierwszego równania do drugiego i mamy

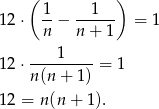
( ) 1- --1--- 12 ⋅ n − n + 1 = 1 12 ⋅----1---- = 1 n(n + 1) 12 = n (n + 1).

Ponieważ prawa strona jest rosnącą funkcją zmiennej naturalnej n , powyższe równanie może mieć tylko jedno rozwiązanie, więc musi być n = 3 .  
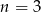Odpowiedź: W ciągu 3 godzin.

Wersja PDF