/Konkursy

Zadanie nr 8898720

Dodaj do ulubionych
Dodaj do rozwiązanych

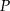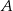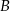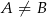Dwa okręgi są styczne zewnętrznie w punkcie P . Poprowadzono prostą, styczną do obu okręgów odpowiednio w punktach A i B (A ⁄= B ). Wykaż, że kąt 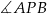∡AP B jest prosty.

Rozwiązanie

Zacznijmy od rysunku.

PIC

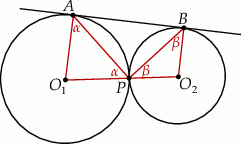
Zauważmy, że

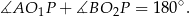
∡AO 1P + ∡BO 2P = 180∘.

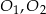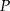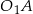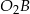Tak jest, bo punkty O 1,O 2 i P leżą na jednej prostej, oraz odcinki O 1A i O 2B są do siebie równoległe (bo oba są prostopadłe do prostej AB )

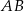Sposób I

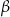Jeżeli oznaczymy kąty α i β jak na rysunku, to powyższą równość możemy zapisać jako

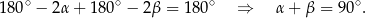
180∘ − 2α + 180 ∘ − 2 β = 180 ∘ ⇒ α+ β = 90 ∘.

Z drugiej strony,

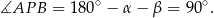
∘ ∘ ∡AP B = 180 − α − β = 90 .

Sposób II

Tym razem skorzystamy z twierdzenia o stycznej.

PIC

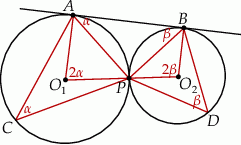
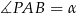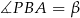Jeżeli oznaczymy ∡PAB = α i ∡P BA = β , to na mocy twierdzenia o stycznej,

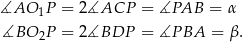
∡AO 1P = 2∡ACP = ∡PAB = α ∡BO P = 2∡BDP = ∡P BA = β. 2

Stąd

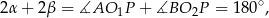
∘ 2 α+ 2β = ∡AO 1P + ∡BO 2P = 1 80 ,

czyli 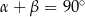∘ α + β = 90 . To oczywiście oznacza, że trójkąt 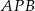AP B jest prostokątny.

Wersja PDF