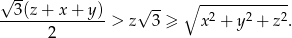Zadanie nr 9721241
Wykaż, że jeżeli 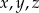 są długościami boków trójkąta to
są długościami boków trójkąta to 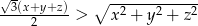 .
.
Rozwiązanie
Bez zmniejszania ogólności możemy założyć, że 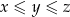 . Korzystając z tego założenia mamy
. Korzystając z tego założenia mamy
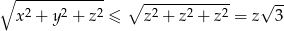
Ponieważ 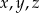 są bokami trójkąta, więc
są bokami trójkąta, więc 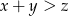 . Mamy stąd
. Mamy stąd
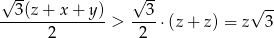
Mamy zatem
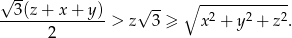
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli 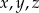 są długościami boków trójkąta to
są długościami boków trójkąta to 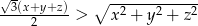 .
.
Bez zmniejszania ogólności możemy założyć, że 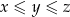 . Korzystając z tego założenia mamy
. Korzystając z tego założenia mamy
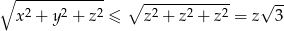
Ponieważ 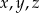 są bokami trójkąta, więc
są bokami trójkąta, więc 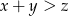 . Mamy stąd
. Mamy stąd
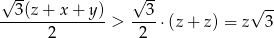
Mamy zatem